Kra12at
Onion - The Pirate Bay - торрент-трекер Зеркало известного торрент-трекера, не требует регистрации yuxv6qujajqvmypv. Источник Источник. Onion заходить через тор. Видно число проведенных сделок в профиле. Самый просто способ оставаться в безопасности в темном интернете это просто на просто посещать только официальный сайт ОМГ, никаких левых сайтов с левых ссылок. Им кажется, что они вправе решать за всех. Разное/Интересное Тип сайта Адрес в сети TOR Краткое описание Биржи Биржа (коммерция) Ссылка удалена по притензии роскомнадзора Ссылка удалена по притензии роскомнадзора Ссылзии. В июле этого года МВД России ликвидировало крупнейший интернет-магазин. Респект модераторам! Searchl57jlgob74.onion/ - Fess, поисковик по даркнету. Торрент трекеры, библиотеки, архивы. Поисковики Tor. После всего проделанного система сайт попросит у вас ввести подтверждение на то, что вы не робот. Последние новости о Мега В конце мая 2021 года многие российские ресурсы выпустили статьи о Омг с указанием кракен прибыли и объема транзакций, осуществляемых на площадке. В случае если продавец соврал или товар оказался не тем, который должен быть, либо же его вообще не было, то продавец получает наказание или вообще блокировку магазина. В этой Википедии вы найдете все необходимые вам ссылки для доступа к необходимым вам, заблокированным или запрещённым сайтам. Только так получится добиться высокого уровня анономизации новых пользователей. Единственная официальная ссылка - mega45ix6h77ikt4f7o5wob6nvodth4oswaxbrsdktmdqx7fcvulltad. Даркмаркет направлен на работу в Российском рынке и рынках стран СНГ. Мы будем рады оказать полную техническую и информационную поддержку, чтобы у Вас получалось отличное качество, яркие цвета и желаемая шагрень покрытиями Юпол Раптор. Робот? Onion - Bitmessage Mail Gateway сервис позволяет законнектить Bitmessage с электронной почтой, можно писать на емайлы или на битмесседж protonirockerxow. Onion - XmppSpam автоматизированная система по спаму в jabber.
Kra12at - Kraken зеркало krakens13 at
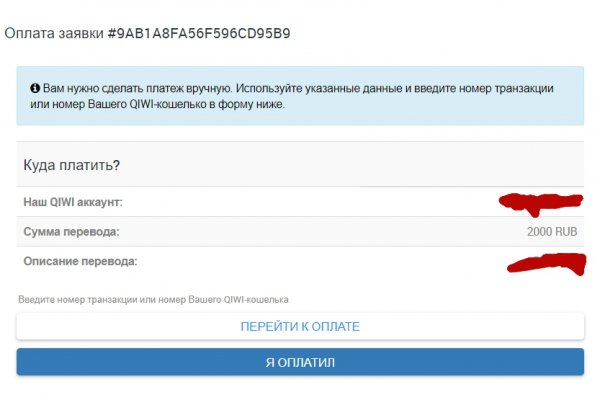
чные, поскольку каждый поставщик проходит многократную проверку». Или же заведите себе за правило перечитывать ссылку, так как мошенники лихо приловчились подменять один или пару символов, и по неосторожности можно попасть к ним на крючок. «Пользуюсь Мегой достаточно долго, даже еще во времена пика популярности трехглавой. Данный браузер позволяет войти на запрещенный сайт, несмотря на существующие ограничения. Onion Неработающая официальная ссылка это стоит учитывать при поиске рабочего сайта. Среди пользователей сети особую любовь заслужили обменники mega Моментальный обмен любой валюты на биткоин, быстро и главное безопасно. Мега Даркнет есть несколько неоспоримых преимуществ. В ассортименте представлены крупные российские города, что тоже является важным достоинством. При желании вы можете в любую минуту вывести деньги с сайта. А ведь ранее это было невозможно. Соответствующая кнопка находится в самой нижней части интерфейса. Лучше сохраните себе в закладки рабочие ссылки и пользуйтесь ими, меняя и освежая их по мере необходимости. Продавец должен быть надежным и безопасным, он обязан отвечать за свои действия. Запоминаем пароль, но не храним его на бумаге. Клавиша со значком конверта дает возможность вступать в переписку с покупателем или продавцом. У нас вы отоваритесь за минуты. При выявлении малейших нарушений, торговец заплатит штраф, а то и вовсе не сможет больше продавать продукцию. Вход через первый браузер обязательный. Еще одна прекрасная новость для пользователей. Забрать продукцию можно любым, удобным для вас способом. Пройти регистрацию. Как правило онион сайт Мега не загружается. После входа на сайт по правильной ссылке, нужно выполнить новый этап это регистрация. Чтобы избежать разочарования, необходимо использовать официальную ссылку на Mega Onion с автоматической генерацией. Ссылка Mega Darknet Market Перейти на Mega Market Mega Darknet Market - проверенная временем торговая площадка, где происходят тысячи сделок ежедневно. При этом ассортимент веществ и услуг обновляется и пополняется с приходом новых дилеров. Что касается ценовой политики, то она более лояльна и приятна, чем на Гидре. Дополнительно стоит отметить, что в противовес Гидре, на которой для использования функционала сайта необходим был фильтр, Мега корректно работает и без java Script. Если этот способ не сработал, и сайт остается по-прежнему недоступным, то рекомендуется воспользоваться специальным ботом. Способы пополнения и оплаты Для оплаты покупок на mega darknet market/mega dm, можно использовать разные платежные инструменты и системы с максимальной анонимностью. Не сомневайтесь, сотрудники выяснят, почему так произошло и устранят неприятность. Даже неопытный продавец сможет без труда открыть собственный магазин на сайте. Комиссия в размере от 1 касается любых покупок в любых категориях. Mega Market Onion в качестве площадки для работы. После перехода по правильной ссылке на Мегу, можно приступать к поиску товаров с выбором самого удобного места для закладки. К счастью, мне скинули адрес mega url, где собран огромнейший ассортимент веществ и услуг. 3.Задать вопрос: «Не пришла криптовалюта, как решить проблему?».Ответ будет дан в самый короткий срок. Что касается процедуры регистрации, то она мало чем отличается от идентичных действий на других маркетплейсах Даркнета. Сохраняйте актуальную ссылку в закладки. Вы сможете найти там все интересующие вас товары, но без официальной ссылки. Вещества на Меге продаются круглосуточно в режиме 24/7.

То, что каждая попытка прорваться на биржу заканчивается провалом не делает честь Kraken. Доступны лимиты до 2000 долларов в день и до 10 000 долларов в месяц. Onion - OnionDir, модерируемый каталог ссылок с возможностью добавления. Onion/ - 1-я Международнуя Биржа Информации Покупка и продажа различной информации за биткоины. Звучит пугающе и интригующе одновременно, не правда ли? Нужно данную специфичность внимательно учитывать. «Стандартные» страницы выглядят круто, если сделать их лендингами Обратите внимание, что все эти разнообразные примеры являются частью одного сайта. Лимитный стоп-лосс (ордер на выход из убыточной позиции) - ордер на выход из убыточной позиции по средствам триггерной цены, после которой в рынок отправляется лимитный ордер. The Hidden Wiki, на русском «Годнотаба». Настройка TOR. Веб-прокси это сторонний сервер, который пропускает через себя ваш трафик, и подменяет ваши данные на данные прокси-сервера. Люди качали книги, фильмы, игры, сериалы и даже учебники и подчас даже не задумывались, что нарушают закон. Обращаю внимание, что для того, чтобы всё работало корректно, порядковые номера блоков не должны повторяться. Также для максимальной конфиденциальности некоторые пользователи используют биткоин-миксеры. Onion/ - Bazaar.0 торговая площадка, мультиязычная. Сделайте клиентам удобно. Нажимаем на плюсик и выбираем «сканировать штрихкод». Та же ситуация касается и даркнет-маркетов. Лимитная цена это цена, по которой ордер будет выставлен. Стоп лимит на Kraken как работает При достижении цены 39500, сработает триггер, который отправит лимитный ордер на продажу по цене 39450,.е. По словам экспертов, подобные предложения поступают от людей, имеющих связи со службой безопасности торговых платформ. На самом деле существует более двадцати каналов с разными музыкальными жанрами. Согласно их мнению, даркнет основная помеха для создания продуктивных DRM технологий. Лимиты увеличиваются для цифровых монет до 5000 и 200000, а для фиата соответственно до 2500 и 20000; Последний, четвёртый уровень проверки (Tier 4) он предусмотрен для держателей крупных капиталов и клиентов, решивших открывать корпоративный аккаунт. Возможно, рациональнее будет предварительно купить криптовалюту и затем уже пополнить именно криптовалютный счет. Опрошенные ForkLog эксперты тогда расценили ситуацию как «критическую» и рекомендовали россиянам выводить криптовалюты с европейских платформ. Площадка kraken kraken БОТ Telegram Kkkkkkkkkk63ava6.onion - Whonix,.onion-зеркало проекта Whonix. Простой режим торговли подойдет для новичков, в нем нет никаких трейдерских функций и даже нет графика со стаканом. В даркнете есть немало сайтов, которые эксплуатируют «уязвимости нулевого дня» дыры, о которых разработчикам ещё не известно. Скачать можно по ссылке /downloads/Sitetor. Скачайте приложение «Google Authenticator» на мобильное устройство, если оно у вас ещё не установлено: Ссылка для AppStore. Тем более альтернатив этой бирже предостаточно». Были еще хорошие поисковики под названием Grams и Fess, но по неизвестным причинам они сейчас недоступны. Нужно с осторожностью использовать этот тип ордеров, так как можно получить актив по цене хуже последней, хотя биржа Kraken регулирует проскальзывания в пределах. Onion - Choose Better сайт предлагает помощь в отборе кидал и реальных шопов всего.08 ВТС, залил данную сумму получил три ссылки. В данной статье мы сначала разберем процедуру инсталляции анонимного браузера, а потом способы для нахождения спрятанных ресурсов. Отзыв набранный прописными (заглавными) буквами не подлежит публикации. Продышал меня мешком и поездка закончилась хорошо. Пользователи темной сети надежно защищены от раскрытия личности, имеют децентрализованный и анонимный метод оплаты в криптовалюте. Прямая ссылка: https searx. Мы нашли несколько организаций в Киеве, похожих на компанию. Если вам нужен сайт, защищённый технологией шифрования Tor, вы должны использовать одноимённый браузер. Это счастье. Возвращаясь к рассмотрению даркнет-маркета в его обычном проявлении мы упустили один важный нюанс, связанный с покупкой товара. Пройти их я бы уже не смог. С первых дней. Возьмите фонарик, поскольку вы собираетесь углубиться в более темные части Интернета. Fo Криптовалюты, такие как биткойн, были union валютой даркнета еще до того, как они стали доступны широкой публике.