Infinitezimalni nizovi – definicija i svojstva. Primjeri Koja se količina naziva infinitezimalnom
Račun infinitezimalnih i velikih
Infinitezimalni račun- proračuni koji se izvode s infinitezimalnim veličinama, u kojima se izvedeni rezultat smatra beskonačnim zbrojem infinitezimalnih veličina. Račun infinitezimala opći je pojam za diferencijalni i integralni račun koji čini osnovu moderne više matematike. Pojam infinitezimalne količine usko je povezan s pojmom granice.
Infinitezimalno
Naknadna slijed a n nazvao infinitezimalnog, Ako . Na primjer, niz brojeva je infiniteziman.
Funkcija se zove infinitezimalna u blizini točke x 0 ako ![]() .
.
Funkcija se zove infinitesimal u beskonačnosti, Ako ![]() ili
ili ![]() .
.
Također infinitezimalna je funkcija koja je razlika između funkcije i njezine granice, odnosno if ![]() , To f(x) − a = α( x)
, .
, To f(x) − a = α( x)
, .
Beskrajno velika količina
U svim formulama ispod, podrazumijeva se da beskonačnost desno od jednakosti ima određeni predznak (bilo "plus" ili "minus"). To je npr. funkcija x grijeh x, neograničen s obje strane, nije beskonačno velik na .
Naknadna slijed a n nazvao beskrajno velika, Ako ![]() .
.
Funkcija se zove beskonačno velika u blizini točke x 0 ako ![]() .
.
Funkcija se zove beskonačno velik u beskonačnosti, Ako ![]() ili
ili ![]() .
.
Svojstva beskonačno malog i beskonačno velikog
Usporedba infinitezimalnih veličina
Kako usporediti infinitezimalne količine?
Omjer infinitezimalnih veličina čini tzv. nesigurnost.
Definicije
Pretpostavimo da imamo infinitezimalne vrijednosti α( x) i β( x) (ili, što za definiciju nije bitno, infinitezimalni nizovi).
Za izračun takvih granica prikladno je koristiti L'Hopitalovo pravilo.
Usporedni primjeri
Korištenje OKO-simbolika, dobiveni rezultati mogu se napisati u sljedećem obliku x 5 = o(x 3). U ovom slučaju, sljedeći unosi su istiniti: 2x 2 + 6x = O(x) I x = O(2x 2 + 6x).Ekvivalentne vrijednosti
Definicija
Ako , tada se infinitezimalne veličine α i β nazivaju ekvivalent ().
Očito je da su ekvivalentne količine poseban slučaj infinitezimalnih veličina istog reda malenosti.
Kada vrijede sljedeći odnosi ekvivalencije (kao posljedice tzv. izvanrednih granica):
Teorema
Granica kvocijenta (omjera) dviju infinitezimalnih veličina neće se promijeniti ako se jedna od njih (ili obje) zamijeni ekvivalentnom količinom.Ovaj teorem ima praktično značenje pri pronalaženju granica (vidi primjer).
Primjer upotrebe
Zamjena sjan 2x ekvivalentna vrijednost 2 x, dobivamoPovijesna crtica
O konceptu "infinitezimalnog" raspravljalo se još u antičko doba u vezi s konceptom nedjeljivih atoma, ali nije bio uključen u klasičnu matematiku. Ponovno je oživljena dolaskom "metode nedjeljivih" u 16. stoljeću - dijeljenjem figure koja se proučava u infinitezimalne dijelove.
U 17. stoljeću došlo je do algebraizacije infinitezimalnog računa. Počele su se definirati kao numeričke veličine koje su manje od bilo koje konačne (različite od nule) količine, a opet nisu jednake nuli. Umijeće analize sastojalo se u sastavljanju relacije koja sadrži infinitezimalne vrijednosti (diferencijale) i zatim njenom integriranju.
Matematičari stare škole stavili su koncept na test infinitezimalnog oštra kritika. Michel Rolle je napisao da je novi račun " skup genijalnih grešaka"; Voltaire je zajedljivo primijetio da je račun umijeće računanja i točnog mjerenja stvari čije se postojanje ne može dokazati. Čak je i Huygens priznao da ne razumije značenje diferencijala višeg reda.
Kao ironija sudbine može se smatrati pojava sredinom stoljeća nestandardne analize, koja je dokazala da je izvorno gledište - stvarne infinitezimale - također dosljedno i da se može koristiti kao osnova za analizu.
vidi također
Zaklada Wikimedia. 2010.
Pogledajte što je "infinitezimalna količina" u drugim rječnicima:
BESKRAJNO MALA KOLIČINA- promjenljiva veličina u nekom procesu, ako se u tom procesu beskonačno približava (teži) nuli... Velika politehnička enciklopedija
Infinitezimalno- ■ Nešto nepoznato, a vezano za homeopatiju... Leksikon običnih istina
BESKONAČNO MALE FUNKCIJE I NJIHOVA OSNOVNA SVOJSTVA
Funkcija y=f(x) nazvao infinitezimalnog na x→a ili kada x→∞, ako ili , tj. infinitezimalna funkcija je funkcija čija je granica u danoj točki nula.
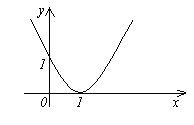
Primjeri.
Uspostavimo sljedeći važan odnos:
Teorema. Ako funkcija y=f(x) reprezentativan sa x→a kao zbroj konstantnog broja b i infinitezimalne veličine α(x): f (x)=b+ α(x) to .
Obrnuto, ako je , tada f (x)=b+α(x), Gdje sjekira)– infinitezimalno pri x→a.
Dokaz.
Razmotrimo osnovna svojstva infinitezimalnih funkcija.
Teorem 1. Algebarski zbroj dva, tri i općenito bilo kojeg konačnog broja infinitezimala je infinitezimalna funkcija.
Dokaz. Dajmo dokaz za dva pojma. Neka f(x)=α(x)+β(x), gdje i . Moramo dokazati da za bilo koje proizvoljno malo ε > 0 pronađeno δ> 0, tako da za x, zadovoljavajući nejednakost |x – a|<δ , izvedena |f(x)|< ε.
Dakle, fiksirajmo proizvoljan broj ε > 0. Budući da prema uvjetima teorema α(x) je infinitezimalna funkcija, onda postoji takav δ 1 > 0, što je |x – a|< δ 1 imamo |α(x)|< ε / 2. Isto tako, budući da β(x) je infinitezimalno, onda postoji takav δ 2 > 0, što je |x – a|< δ 2 imamo | β(x)|< ε / 2.
Idemo uzeti δ=min(δ 1 , δ2 } .Onda u susjedstvu točke a radius δ svaka od nejednakosti će biti zadovoljena |α(x)|< ε / 2 i | β(x)|< ε / 2. Stoga će u ovom susjedstvu biti
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
oni. |f(x)|< ε, što je i trebalo dokazati.
Teorem 2. Umnožak infinitezimalne funkcije sjekira) za ograničenu funkciju f(x) na x→a(ili kada x→∞) je infinitezimalna funkcija.
Dokaz. Budući da funkcija f(x) je ograničen, onda postoji broj M takav da za sve vrijednosti x iz neke okoline točke a|f(x)|≤M.Štoviše, budući da sjekira) je infinitezimalna funkcija na x→a, tada za proizvoljan ε > 0 postoji okolina točke a, u kojem će vrijediti nejednakost |α(x)|< ε /M. Zatim u manjim od ovih četvrti koje imamo | αf|< ε /M= ε. A ovo znači to af– infinitezimalno. Za tu priliku x→∞ dokaz se provodi na sličan način.
Iz dokazanog teoreme slijedi:
Korolar 1. Ako i, onda.
Korolar 2. Ako c= const, tada .
Teorem 3. Omjer infinitezimalne funkcije α(x) po funkciji f(x), čija je granica različita od nule, je infinitezimalna funkcija.
Dokaz. Neka ![]() . Zatim 1 /f(x) postoji ograničena funkcija. Stoga razlomak
. Zatim 1 /f(x) postoji ograničena funkcija. Stoga razlomak ![]() je umnožak infinitezimalne funkcije i ograničene funkcije, tj. funkcija je infinitezimalna.
je umnožak infinitezimalne funkcije i ograničene funkcije, tj. funkcija je infinitezimalna.
ODNOS IZMEĐU BESKONAČNO MALIH I BESKONAČNO VELIKIH FUNKCIJA
Teorem 1. Ako funkcija f(x) je beskonačno velik na x→a, zatim funkcija 1 /f(x) je infinitezimalna na x→a.
Dokaz. Uzmimo proizvoljan broj ε >0 i pokazati da za neke δ>0 (ovisno o ε) za sve x, za koji |x – a|<δ , nejednakost je zadovoljena, a to će značiti da 1/f(x) je infinitezimalna funkcija. Doista, budući da f(x) je beskonačno velika funkcija na x→a, onda će biti δ>0 takav da čim |x – a|<δ , dakle | f(x)|> 1/ ε. Ali onda za isto x.
Primjeri.
Može se dokazati i obrnuti teorem.
Teorem 2. Ako funkcija f(x)- infinitezimalno pri x→a(ili x→∞) i onda ne nestaje y= 1/f(x) je beskonačno velika funkcija.
Provedite sami dokaz teorema.
Primjeri.
Dakle, najjednostavnija svojstva infinitezimalnih i beskonačno velikih funkcija mogu se napisati pomoću sljedećih uvjetnih odnosa: A≠ 0
GRANIČNI TEOREMI
Teorem 1. Limes algebarskog zbroja dviju, triju i općenito određenog broja funkcija jednak je algebarskom zbroju limesa tih funkcija, tj.
Dokaz. Provedimo dokaz za dva člana, jer se to može učiniti na isti način za bilo koji broj članova. Neka ![]() .Zatim f(x)=b+α(x) I g(x)=c+β(x), Gdje α
I β
– infinitezimalne funkcije. Stoga,
.Zatim f(x)=b+α(x) I g(x)=c+β(x), Gdje α
I β
– infinitezimalne funkcije. Stoga,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Jer b+c je konstanta i α(x) + β(x) je tada infinitezimalna funkcija
Primjer. .
Teorem 2. Limit umnoška dviju, tri i općenito konačnog broja funkcija jednak je umnošku limesa tih funkcija:
Dokaz. Neka ![]() . Stoga, f(x)=b+α(x) I g(x)=c+β(x) I
. Stoga, f(x)=b+α(x) I g(x)=c+β(x) I
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Raditi prije Krista postoji konstantna vrijednost. Funkcija bβ + c α + αβ na temelju svojstava infinitezimalnih funkcija postoji infinitezimalna količina. Zato .
Korolar 1. Konstantni faktor može se uzeti preko graničnog znaka:
![]() .
.
Korolar 2. Granica stupnja jednaka je graničnom stupnju:
![]() .
.
Primjer.![]() .
.
Teorem 3. Limes kvocijenta dviju funkcija jednak je kvocijentu limesa tih funkcija ako je limes nazivnika različit od nule, tj.
 .
.
Dokaz. Neka . Stoga, f(x)=b+α(x) I g(x)=c+β(x), Gdje α, β – infinitezimalno. Razmotrimo kvocijent
Razlomak je infinitezimalna funkcija jer je brojnik infinitezimalna funkcija, a nazivnik ima granicu c 2 ≠0.
Primjeri.

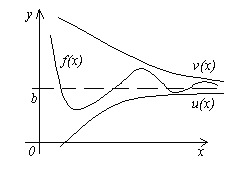
Teorem 4. Neka su zadane tri funkcije f(x), u(x) I v(x), zadovoljavajući nejednakosti u (x)≤f(x)≤ v(x). Ako funkcije u(x) I v(x) imaju isto ograničenje na x→a(ili x→∞), zatim funkcija f(x) teži istoj granici, tj. Ako
![]() , To .
, To .
Značenje ove teoreme je jasno sa slike.
Dokaz teorema 4 može se naći, na primjer, u udžbeniku: Piskunov N. S. Diferencijalni i integralni račun, sv. 1 - M.: Nauka, 1985.
Teorem 5. Ako na x→a(ili x→∞) funkcija y=f(x) prihvaća nenegativne vrijednosti y≥0 a ujedno teži granici b, tada ova granica ne može biti negativna: b≥0.
Dokaz. Provest ćemo dokaz kontradikcijom. Hajdemo to pretvarati b<0 , Zatim |y – b|≥|b| pa stoga modul razlike ne teži nuli kada x→a. Ali onda g ne doseže granicu b na x→a, što je u suprotnosti s uvjetima teorema.
Teorem 6. Ako dvije funkcije f(x) I g(x) za sve vrijednosti argumenta x zadovoljiti nejednakost f(x)≥ g(x) i imaju granice, tada nejednakost vrijedi b≥c.
Dokaz. Prema uvjetima teorema f(x)-g(x) ≥0, dakle, prema teoremu 5 ![]() , ili
, ili ![]() .
.
JEDNOSTRANA OGRANIČENJA

Do sada smo razmatrali određivanje limita funkcije kada x→a na proizvoljan način, tj. granica funkcije nije ovisila o tome kako se nalazi x prema a, lijevo ili desno od a. Međutim, prilično je uobičajeno pronaći funkcije koje nemaju ograničenje pod ovim uvjetom, ali imaju ograničenje ako x→a, ostajući na jednoj strani A, lijevo ili desno (vidi sliku). Stoga se uvode pojmovi jednostranih granica.
Ako f(x) teži do granice b na x teži određenom broju a Tako x prihvaća samo vrijednosti manje od a, pa pišu i zovu granica funkcije f(x) u točki a na lijevoj strani.
Račun infinitezimalnih i velikih
Infinitezimalni račun- proračuni koji se izvode s infinitezimalnim veličinama, u kojima se izvedeni rezultat smatra beskonačnim zbrojem infinitezimalnih veličina. Račun infinitezimala opći je pojam za diferencijalni i integralni račun koji čini osnovu moderne više matematike. Pojam infinitezimalne količine usko je povezan s pojmom granice.
Infinitezimalno
Naknadna slijed a n nazvao infinitezimalnog, Ako . Na primjer, niz brojeva je infiniteziman.
Funkcija se zove infinitezimalna u blizini točke x 0 ako ![]() .
.
Funkcija se zove infinitesimal u beskonačnosti, Ako ![]() ili
ili ![]() .
.
Također infinitezimalna je funkcija koja je razlika između funkcije i njezine granice, odnosno if ![]() , To f(x) − a = α( x)
, .
, To f(x) − a = α( x)
, .
Beskrajno velika količina
Naknadna slijed a n nazvao beskrajno velika, Ako ![]() .
.
Funkcija se zove beskonačno velika u blizini točke x 0 ako ![]() .
.
Funkcija se zove beskonačno velik u beskonačnosti, Ako ![]() ili
ili ![]() .
.
U svim slučajevima podrazumijeva se da beskonačnost desno od jednakosti ima određeni predznak (bilo "plus" ili "minus"). To je npr. funkcija x grijeh x nije beskonačno velik na .
Svojstva beskonačno malog i beskonačno velikog
Usporedba infinitezimalnih veličina
Kako usporediti infinitezimalne količine?
Omjer infinitezimalnih veličina čini tzv. nesigurnost.
Definicije
Pretpostavimo da imamo infinitezimalne vrijednosti α( x) i β( x) (ili, što za definiciju nije bitno, infinitezimalni nizovi).
Za izračun takvih granica prikladno je koristiti L'Hopitalovo pravilo.
Usporedni primjeri
Korištenje OKO-simbolika, dobiveni rezultati mogu se napisati u sljedećem obliku x 5 = o(x 3). U ovom slučaju, sljedeći unosi su istiniti: 2x 2 + 6x = O(x) I x = O(2x 2 + 6x).Ekvivalentne vrijednosti
Definicija
Ako , tada se infinitezimalne veličine α i β nazivaju ekvivalent ().
Očito je da su ekvivalentne količine poseban slučaj infinitezimalnih veličina istog reda malenosti.
Kada vrijede sljedeći odnosi ekvivalencije: , , ![]() .
.
Teorema
Granica kvocijenta (omjera) dviju infinitezimalnih veličina neće se promijeniti ako se jedna od njih (ili obje) zamijeni ekvivalentnom količinom.Ovaj teorem ima praktično značenje pri pronalaženju granica (vidi primjer).
Primjer upotrebe
Zamjena sjan 2x ekvivalentna vrijednost 2 x, dobivamoPovijesna crtica
O konceptu "infinitezimalnog" raspravljalo se još u antičko doba u vezi s konceptom nedjeljivih atoma, ali nije bio uključen u klasičnu matematiku. Ponovno je oživljena dolaskom "metode nedjeljivih" u 16. stoljeću - dijeljenjem figure koja se proučava u infinitezimalne dijelove.
U 17. stoljeću došlo je do algebraizacije infinitezimalnog računa. Počele su se definirati kao numeričke veličine koje su manje od bilo koje konačne (različite od nule) količine, a opet nisu jednake nuli. Umijeće analize sastojalo se u sastavljanju relacije koja sadrži infinitezimalne vrijednosti (diferencijale) i zatim njenom integriranju.
Matematičari stare škole stavili su koncept na test infinitezimalnog oštra kritika. Michel Rolle je napisao da je novi račun " skup genijalnih grešaka"; Voltaire je zajedljivo primijetio da je račun umijeće računanja i točnog mjerenja stvari čije se postojanje ne može dokazati. Čak je i Huygens priznao da ne razumije značenje diferencijala višeg reda.
Sporovi u Pariškoj akademiji znanosti oko opravdanosti analize postali su toliko skandalozni da je Akademija jednom potpuno zabranila svojim članovima govoriti o ovoj temi (to se prije svega odnosilo na Rollea i Varignona). Godine 1706. Rolle je javno povukao svoje prigovore, ali su se rasprave nastavile.
Godine 1734. slavni engleski filozof, biskup George Berkeley, objavio je senzacionalni pamflet, poznat pod skraćenim naslovom “ Analitičar" Njegovo puno ime: " Analitičar ili diskurs upućen matematičaru koji ne vjeruje, gdje se ispituje jesu li predmet, načela i zaključci moderne analize jasnije uočeni ili jasnije izvedeni od vjerskih sakramenata i članaka vjere».
Analitičar je sadržavao duhovitu i uglavnom poštenu kritiku infinitezimalnog računa. Berkeley je smatrao da metoda analize nije u skladu s logikom i napisao je da, " koliko god bila korisna, može se smatrati samo nekom vrstom nagađanja; spretna vještina, umjetnost ili bolje reći trik, ali ne kao metoda znanstvenog dokazivanja" Citirajući Newtonovu frazu o porastu trenutnih količina "na samom početku njihova nastanka ili nestanka", Berkeley ironizira: " nisu niti konačne količine, niti infinitezimali, niti čak ništa. Zar ih ne bismo mogli nazvati duhovima preminulih veličina?... I kako uopće možemo govoriti o odnosu između stvari koje nemaju veličinu?.. Svatko tko može probaviti drugu ili treću fluksiju [derivat], drugu ili treću razliku, ne bi trebalo, kako mi se čini, nešto zamjeriti teologiji».
Nemoguće je, piše Berkeley, zamisliti trenutnu brzinu, odnosno brzinu u danom trenutku i u danoj točki, jer koncept gibanja uključuje koncepte (konačnog različitog od nule) prostora i vremena.
Kako analiza daje točne rezultate? Berkeley je došao na ideju da se to može objasniti prisutnošću nekoliko pogrešaka u analitičkim zaključcima, te je to ilustrirao primjerom parabole. Zanimljivo je da su se neki veliki matematičari (primjerice Lagrange) složili s njim.
Nastala je paradoksalna situacija kada su se strogost i plodnost u matematici ispreplitali. Unatoč korištenju nezakonitih radnji s loše definiranim konceptima, broj izravnih pogrešaka bio je iznenađujuće mali - intuicija je priskočila u pomoć. Pa ipak, kroz 18. stoljeće matematička analiza se razvijala brzo, bez ikakvog opravdanja. Njegova je učinkovitost bila nevjerojatna i govorila je sama za sebe, ali značenje diferencijala još uvijek nije bilo jasno. Osobito su se često brkali infinitezimalni prirast funkcije i njezin linearni dio.
Kroz 18. stoljeće ulagani su golemi napori da se stanje popravi, au njima su sudjelovali najbolji matematičari stoljeća, no tek je Cauchy početkom 19. stoljeća uspio uvjerljivo izgraditi temelje analize. Strogo je definirao osnovne pojmove - limit, konvergencija, kontinuitet, diferencijal itd., nakon čega su stvarne infinitezimale nestale iz znanosti. Neke preostale suptilnosti objašnjene su kasnije
Teorem 2.4. Ako nizovi (x n) i (y n) konvergiraju i x n ≤ y n, n > n 0, tada je lim x n ≤ lim y n.
Neka je lim xn = a, |
lim yn = b i a > b. Po definiciji 2.4 granice |
||||||||||||||||||||
nizovi po broju ε = |
postoji broj N takav da |
||||||||||||||||||||
Prema tome, n > max(n0 , N) yn< |
< xn , что противоречит |
||||||||||||||||||||
stanje. |
|||||||||||||||||||||
Komentar. Ako nizovi (xn), (yn) konvergiraju za |
|||||||||||||||||||||
sve n > n0 |
xn< yn , то можно утверждать лишь, что lim xn |
≤ lim yn . |
|||||||||||||||||||
Da biste to vidjeli, dovoljno je razmotriti nizove
i yn = |
||||
Sljedeći rezultati slijede izravno iz definicije 2.4.
Teorem 2.5. Ako brojevni niz (x n) konvergira i lim x n< b (b R), то N N: x n < b, n >N.
Posljedica. Ako niz (xn) konvergira i lim xn 6= 0, tada
N N: sgn xn = sgn(lim xn), n > N.
Teorem 2.6. Neka nizovi (x n), (y n), (z n) zadovoljavaju uvjete:
1) x n ≤ yn ≤ zn, n > n0,
2) sekvence(x n) i (z n) konvergiraju i lim x n = lim z n = a.
Tada niz (y n ) konvergira i lim y n = a.
2.1.3 Infinitezimalni nizovi
Definicija 2.7. Niz brojeva (x n) naziva se infinitezimalnim (infinitezimalnim) ako konvergira i lim x n = 0.
Prema definiciji 2.4 granice niza brojeva, definicija 2.7 je ekvivalentna sljedećem:
Definicija 2.8. Niz brojeva (x n) naziva se infinitezimalnim ako za bilo koji pozitivan broj ε postoji broj N = N(ε) takav da za sve n > N elementi x n tog niza zadovoljavaju nejednakost |x n |< ε.
Dakle, (xn) - b.m. ε > 0 N = N(ε) : n > N |xn |< ε.
Iz primjera 2, 3 i napomene 1 uz teorem 2.3 dobivamo da nakon
valjanost ( |
q−n |
su beskonačni |
||||||||||||
Svojstva infinitezimalnih nizova opisana su sljedećim teoremima.
Teorem 2.7. Zbroj konačnog broja infinitezimalnih nizova je infinitezimalni niz.
Neka su nizovi (xn), (yn) infinitezimalni. Pokažimo da će (xn + yn) također biti jedan. Postavimo ε > 0. Tada postoji broj
N1 = N1 (ε) tako da je |
||||
|xn |< |
N>N1, |
|||
a postoji broj N2 = N2 (ε) takav da |
||||
|yn |< |
N>N2. |
|||
Označimo s N = max(N1, N2). Za n > N vrijedit će nejednakosti (2.1) i (2.2). Prema tome, za n > N
|xn + yn | ≤ |xn | + |yn |< 2 + 2 = ε.
To znači da je niz (xn +yn) infinitezimalan. Tvrdnja o zbroju konačnog broja infinitezimalnih nizova
To slijedi iz onoga što je dokazano indukcijom.
Teorem 2.8. Umnožak infinitezimalnog niza i ograničenog niza je infinitezimalan.
Neka je (xn) ograničen i (yn) infinitezimalni niz. Prema definiciji 2.6 ograničenog niza postoji broj M > 0 takav da je
|xn | ≤ M, n N. |
Fiksirajmo proizvoljan broj ε > 0. Budući da je (yn) infinitezimalni niz, postoji broj N = N(ε) takav da je
Stoga niz (xn yn ) je infinitezimalna.

Korolar 1. Umnožak infinitezimalnog niza i konvergentnog niza je infinitezimalni niz.
Korolar 2. Umnožak dva infinitezimalna niza je infinitezimalni niz.
Koristeći infinitezimalne nizove, definicija konvergentnog niza može se drugačije promatrati.
Lema 2.1. Da bi broj a bio limit numeričkog niza (x n), potrebno je i dovoljno da postoji prikaz x n = a + α n, n N, u kojem je (α n) infinitezimalni niz.
Nužnost. Neka je lim xn = a i a R. Tada
ε > 0 N = N(ε) N: n > N |xn − a|< ε.
Ako postavimo αn = xn − a, n N, tada dobivamo da je (αn) infinitezimalni niz i xn = a + αn, n N.
Adekvatnost. Neka je niz (xn) takav da postoji broj a za koji je xn = a + αn, n N, i lim αn = 0. Fiksirajmo proizvoljan pozitivan broj ε. Kako je lim αn = 0, onda postoji broj N = N(ε) N takav da je |αn |< ε, n >N. To jest, u drugim zapisima, n > N |xn − a|< ε. Это означает, что lim xn = a.
Primijenimo lemu 2.1 na važan poseban primjer.
Lema 2.2. lim n n = 1.
√ √
Budući da je za sve n > 1 n n > 1, tada je n n = 1 + αn , a αn > 0 za
svi n > 1. Stoga je n = (1 + α |
)n = 1 + nα |
+ αn. |
|||||||||||||||
Budući da su svi članovi pozitivni, n |
|||||||||||||||||
Neka je ε > 0. Budući da |
2/n< ε для всех n >2/ε , tada, uz pretpostavku |
||||||||||||||||
N = max(1, ), dobivamo da je 0< αn < ε, n >N. Stoga,
niz (αn) je infinitezimalan i prema lemi
2.1, lim n n = 1. √
Posljedica. Ako je a > 1, onda je lim n a = 1.√ √
Tvrdnja slijedi iz nejednakosti 1< n a ≤ n n , n >[a].
2.1.4 Aritmetičke operacije s nizovima
Koristeći lemu 2.1 i svojstva infinitezimalnih nizova, lako je dobiti teoreme o granicama nizova dobivenih korištenjem aritmetičkih operacija iz konvergentnih nizova.

|b| 3|b|
2 < |y n | < 2
Teorem 2.9. Neka nizovi brojeva (x n) i (y n) konvergiraju. Tada vrijede sljedeće tvrdnje:
1) niz (x n ± y n ) konvergira i
lim(xn ± yn) = lim xn ± lim yn;
2) niz (x n · y n ) konvergira i
lim(xn · yn ) = lim xn · lim yn ;
3) ako je lim y n 6= 0, tada je omjer x n /y n definiran počevši od
neki broj, niz ( x n ) konvergira i
Prema teoremu 2.8 i korolaru 1, nizovi (a · βn), (b · αn), (αn · βn) su infinitezimalni. Prema teoremu 2.7, niz (aβn + bαn + αn βn ) je infinitezimalan. Tvrdnja 2) slijedi iz reprezentacije (2.5) pomoću leme 2.1.
Prijeđimo na izjavu 3). Prema uvjetu, lim yn = b 6= 0. Na temelju teorema 2.3. niz (|yn |) konvergira i lim |yn | = |b| 6= 0. Dakle, za dan broj ε = |b|/2, postoji broj N takav da je n > N
0 < | 2 b| = |b| −
Prema tome, yn =6 0, i 3|b|< y n < |b| , n >N.
Dakle, kvocijent xn /yn je definiran za sve n > N, a niz (1/yn) je ograničen. Razmotrite razliku za sve n > N
(αn b − aβn ). |
|||||||||||||||||||||
Naknadna slijed |
αn b |
aβn |
Beskonačno mali |
||||||||||||||||||
ograničeno. Prema teoremu 2.8 niz |
|||||||||||||||||||||
− b |
|||||||||||||||||||||
jako malo. Stoga je lemom 2.1 tvrdnja 3) dokazana. Korolar 1. Ako niz (xn) konvergira, tada za bilo koji
Za bilo koji broj c, niz (c · xn ) konvergira i lim(cxn ) = c · lim xn .
Infinitezimalne funkcije
Poziva se funkcija %%f(x)%%. infinitezimalnog(b.m.) s %%x \to a \in \overline(\mathbb(R))%%, ako je uz ovu tendenciju argumenta granica funkcije jednaka nuli.
Koncept b.m. funkcija je neraskidivo povezana s uputama za promjenu svog argumenta. Možemo govoriti o b.m. funkcionira na %%a \to a + 0%% i na %%a \to a - 0%%. Obično b.m. funkcije su označene prvim slovima grčke abecede %%\alpha, \beta, \gamma, \ldots%%
Primjeri
- Funkcija %%f(x) = x%% je b.m. na %%x \to 0%%, jer je njegova granica u točki %%a = 0%% nula. Prema teoremu o povezanosti dvostrane granice i jednostrane granice, ova funkcija je b.m. i s %%x \to +0%% i s %%x \to -0%%.
- Funkcija %%f(x) = 1/(x^2)%% - b.m. na %%x \to \infty%% (kao i na %%x \to +\infty%% i na %%x \to -\infty%%).
Konstantan broj različit od nule, bez obzira koliko malen bio u apsolutnoj vrijednosti, nije b.m. funkcija. Za konstantne brojeve, jedina iznimka je nula, budući da funkcija %%f(x) \equiv 0%% ima ograničenje nule.
Teorema
Funkcija %%f(x)%% ima u točki %%a \in \overline(\mathbb(R))%% produženog brojevnog pravca konačni limit jednak broju %%b%% ako i samo ako je ova funkcija jednaka zbroju ovog broja %%b%% i b.m. funkcije %%\alpha(x)%% s %%x \to a%%, ili $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \lijevodesna strelica \lijevo(f(x) = b + \alpha(x)\desno) \land \lijevo(\lim\granice_(x \to a)(\alpha(x) = 0)\desno). $$
Svojstva infinitezimalnih funkcija
Prema pravilima prijelaza do granice s %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, slijede sljedeće izjave:
- Zbroj konačnog broja b.m. funkcije za %%x \to a%% je b.m. na %%x \to a%%.
- Umnožak bilo kojeg broja b.m. funkcije za %%x \to a%% je b.m. na %%x \to a%%.
Proizvod b.m. funkcije na %%x \to a%% i funkcija ograničena u nekom probušenom susjedstvu %%\stackrel(\circ)(\text(U))(a)%% točke a, postoji b.m. na %%x \na %% funkciju.
Jasno je da je umnožak konstantne funkcije i b.m. kod %%x \to a%% nalazi se b.m. funkcija na %%x \to a%%.
Ekvivalentne infinitezimalne funkcije
Infinitezimalne funkcije %%\alpha(x), \beta(x)%% za %%x \to a%% nazivaju se ekvivalent i napišite %%\alpha(x) \sim \beta(x)%%, ako
$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alpha(x))) = 1. $$
Teorem o zamjeni b.m. funkcije ekvivalentne
Neka su %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% b.m. funkcije za %%x \to a%%, s %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, zatim $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ granice_(x \to a)(\frac(\alpha_1(x))(\beta_1(x))). $$
Ekvivalent b.m. funkcije.
Neka %%\alpha(x)%% bude b.m. funkcija na %%x \to a%%, zatim
- %%\sin(\alpha(x)) \sim \alpha(x)%%
- %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
- %%\tan \alpha(x) \sim \alpha(x)%%
- %%\arcsin\alpha(x) \sim \alpha(x)%%
- %%\arctan\alpha(x) \sim \alpha(x)%%
- %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
- %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
- %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%
Primjer
$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(niz) $$
Beskonačno velike funkcije
Poziva se funkcija %%f(x)%%. beskrajno velika(b.b.) s %%x \to a \in \overline(\mathbb(R))%%, ako s ovom tendencijom argumenta funkcija ima beskonačno ograničenje.
Slično b.m. koncept funkcija b.b. funkcija je neraskidivo povezana s uputama za promjenu argumenta. Možemo govoriti o b.b. funkcije s %%x \to a + 0%% i %%x \to a - 0%%. Pojam “beskonačno velik” ne govori o apsolutnoj vrijednosti funkcije, već o prirodi njezine promjene u blizini dotične točke. Nijedan konstantan broj, ma koliko velik u apsolutnoj vrijednosti, nije beskonačno velik.
Primjeri
- Funkcija %%f(x) = 1/x%% - b.b. na %%x \do 0%%.
- Funkcija %%f(x) = x%% - b.b. na %%x \do \infty%%.
Ako uvjeti definicije $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(niz) $$
onda govore o pozitivan ili negativan b.b. na funkciji %%a%%.
Primjer
Funkcija %%1/(x^2)%% - pozitivno b.b. na %%x \do 0%%.
Veza između b.b. i b.m. funkcije
Ako je %%f(x)%% b.b. s %%x \to a%% funkcijom, zatim %%1/f(x)%% - b.m.
na %%x \to a%%. Ako je %%\alpha(x)%% - b.m. za %%x \to a%% je funkcija različita od nule u nekom probušenom susjedstvu točke %%a%%, tada je %%1/\alpha(x)%% b.b. na %%x \to a%%.
Svojstva beskonačno velikih funkcija
Predstavimo nekoliko svojstava b.b. funkcije. Ova svojstva slijede izravno iz definicije b.b. funkcija i svojstava funkcija koje imaju konačne limite, kao i iz teorema o povezanosti b.b. i b.m. funkcije.
- Umnožak konačnog broja b.b. funkcije za %%x \to a%% je b.b. funkcija na %%x \to a%%. Doista, ako je %%f_k(x), k = \overline(1, n)%% - b.b. funkcije na %%x \to a%%, zatim u nekom probušenom susjedstvu točke %%a%% %%f_k(x) \ne 0%%, i po teoremu o vezi b.b. i b.m. funkcije %%1/f_k(x)%% - b.m. funkcija na %%x \to a%%. Ispada %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m funkcija za %%x \to a%%, i %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funkcija na %%x \to a%%.
- Proizvod b.b. funkcije za %%x \to a%% i funkcija koja je u nekoj punktiranoj okolini točke %%a%% po apsolutnoj vrijednosti veća od pozitivne konstante je b.b. funkcija na %%x \to a%%. Konkretno, proizvod b.b. funkcija s %%x \to a%% i funkcija koja ima konačnu granicu različitu od nule u točki %%a%% bit će b.b. funkcija na %%x \to a%%.
Zbroj dva b.b. funkcije na %%x \to a%% postoji nesigurnost. Ovisno o predznaku članova, priroda promjene takvog zbroja može biti vrlo različita.
Primjer
Neka su zadane funkcije %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. funkcionira na %%x \to \infty%%. Zatim:
- %%f(x) + g(x) = 3x%% - b.b. funkcija na %%x \to \infty%%;
- %%f(x) + h(x) = 0%% - b.m. funkcija na %%x \to \infty%%;
- %%h(x) + v(x) = \sin x%% nema ograničenja na %%x \to \infty%%.
Zbroj funkcije ograničene u nekoj punktiranoj okolini točke %%a%% i b.b. funkcije s %%x \to a%% je b.b. funkcija na %%x \to a%%.
Na primjer, funkcije %%x - \sin x%% i %%x + \cos x%% su b.b. na %%x \do \infty%%.
