Infinitezimális sorozatok – definíció és tulajdonságok. Példák Milyen mennyiséget nevezünk végtelenül kicsinek
Infinitezimálisok és nagyok számítása
Infinitezimális számítás- infinitezimális mennyiségekkel végzett számítások, amelyekben a származtatott eredményt a végtelen kicsinyek végtelen összegének tekintjük. Az infinitezimálisok számítása a differenciál- és integrálszámítás általános fogalma, amely a modern felsőbb matematika alapját képezi. Az infinitezimális mennyiség fogalma szorosan összefügg a határ fogalmával.
Elenyésző
Utóbbi a n hívott elenyésző, Ha . Például egy számsorozat végtelenül kicsi.
A függvényt hívják végtelenül kicsi egy pont közelében x 0 ha ![]() .
.
A függvényt hívják végtelenül kicsi a végtelenben, Ha ![]() vagy
vagy ![]() .
.
Szintén infinitezimális az a függvény, amely a függvény és a határértéke közötti különbség, azaz ha ![]() , Azt f(x) − a = α( x)
, .
, Azt f(x) − a = α( x)
, .
Végtelenül nagy mennyiség
Az összes alábbi képletben az egyenlőségtől jobbra lévő végtelennek egy bizonyos jele van (vagy „plusz” vagy „mínusz”). Ez például a függvény x bűn x, mindkét oldalon korlátlan, nem végtelenül nagy -nál.
Utóbbi a n hívott végtelenül nagy, Ha ![]() .
.
A függvényt hívják végtelenül nagy egy pont közelében x 0 ha ![]() .
.
A függvényt hívják végtelenül nagy a végtelenben, Ha ![]() vagy
vagy ![]() .
.
A végtelenül kicsi és a végtelenül nagy tulajdonságai
Végtelenül kicsi mennyiségek összehasonlítása
Hogyan hasonlítsuk össze a végtelenül kicsi mennyiségeket?
Az infinitezimális mennyiségek aránya alkotja az úgynevezett bizonytalanságot.
Definíciók
Tegyük fel, hogy infinitezimális α( x) és β( x) (vagy ami a definíció szempontjából nem fontos, infinitezimális sorozatok).
Az ilyen határértékek kiszámításához célszerű a L'Hopital-szabályt használni.
Összehasonlítási példák
Használata RÓL RŐL-szimbolika, a kapott eredményeket a következő formában írhatjuk fel x 5 = o(x 3). Ebben az esetben a következő bejegyzések igazak: 2x 2 + 6x = O(x) És x = O(2x 2 + 6x).Egyenértékű értékek
Meghatározás
Ha , akkor az α és β végtelenül kicsiny mennyiségeket nevezzük egyenértékű ().
Nyilvánvaló, hogy az ekvivalens mennyiségek az azonos kicsinységi nagyságrendű végtelenül kicsi mennyiségek speciális esetét jelentik.
Ha a következő ekvivalencia viszonyok érvényesek (az ún. figyelemre méltó határok következményeként):
Tétel
Két végtelenül kicsi mennyiség hányadosának (arányának) határa nem változik, ha az egyiket (vagy mindkettőt) egy ekvivalens mennyiségre cseréljük.Ennek a tételnek gyakorlati jelentősége van a határok megtalálásakor (lásd a példát).
Használati példa
Csere sénn 2x egyenértékű érték 2 x, kapunkTörténelmi vázlat
Az „infinitezimális” fogalmát már az ókorban tárgyalták az oszthatatlan atomok fogalmával kapcsolatban, de a klasszikus matematikában nem szerepelt. A 16. században az „oszthatatlanok módszerének” megjelenésével újjáéledt – a vizsgált figurát végtelenül kis részekre osztva.
A 17. században megtörtént az infinitezimális számítás algebraizálása. Olyan numerikus mennyiségekként kezdték meghatározni őket, amelyek kisebbek bármely véges (nem nulla) mennyiségnél, és mégsem egyenlők nullával. Az elemzés művészete abból állt, hogy felállítottunk egy infinitezimálisokat (differenciálokat) tartalmazó relációt, majd integráltuk azt.
A régi iskola matematikusai próbára teszik a koncepciót elenyésző kemény kritika. Michel Rolle azt írta, hogy az új kalkulus: zseniális hibák halmaza"; Voltaire maróan megjegyezte, hogy a kalkulus olyan dolgok kiszámításának és pontos mérésének művészete, amelyek létezését nem lehet bizonyítani. Még Huygens is elismerte, hogy nem értette a magasabb rendű különbségek jelentését.
A sors iróniájának tekinthető a nem szabványos elemzések század közepén kialakuló megjelenése, amely bebizonyította, hogy az eredeti nézőpont - a tényleges infinitezimálisok - is konzisztens volt, és az elemzés alapjául is használható.
Lásd még
Wikimédia Alapítvány. 2010.
Nézze meg, mi az „infinitezimális mennyiség” más szótárakban:
VÉGTELEN KIS MENNYISÉG- változó mennyiség egy bizonyos folyamatban, ha ebben a folyamatban végtelenül közelít (hajlik) a nullához... Nagy Politechnikai Enciklopédia
Elenyésző- ■ Valami ismeretlen, de a homeopátiához kapcsolódó... Közös igazságok lexikona
VÉGTELEN KIS FUNKCIÓK ÉS ALAPVETŐ TULAJDONSÁGOK
Funkció y=f(x) hívott elenyésző nál nél x→a vagy mikor x→∞, ha vagy , azaz. az infinitezimális függvény olyan függvény, amelynek határértéke egy adott pontban nulla.
Példák.
Hozzuk létre a következő fontos kapcsolatot:
Tétel. Ha a funkció y=f(x)-val reprezentálható x→aállandó szám összegeként bés végtelenül kicsiny nagyságrendű α(x): f(x)=b+ α(x) Az .
Fordítva, ha , akkor f(x)=b+α(x), Ahol fejsze)– végtelenül kicsi at x→a.
Bizonyíték.
Tekintsük az infinitezimális függvények alapvető tulajdonságait.
1. tétel. Kettő, három és általában tetszőleges számú infinitezimális algebrai összege végtelen kicsi függvény.
Bizonyíték. Bizonyítsunk két kifejezésre. Hadd f(x)=α(x)+β(x), hol és . Be kell bizonyítanunk, hogy tetszőleges kis ε esetén > 0 talált δ> 0, olyan, hogy a x, kielégítve az egyenlőtlenséget |x – a|<δ , előadták |f(x)|< ε.
Tehát rögzítsünk egy tetszőleges ε számot > 0. Mivel a tétel feltételei szerint α(x) egy infinitezimális függvény, akkor van ilyen δ 1 > 0, ami |x – a|< δ 1 van |α(x)|< ε / 2. Ugyanígy, mióta β(x) végtelenül kicsi, akkor van ilyen δ 2 > 0, ami |x – a|< δ 2 van | β(x)|< ε / 2.
Vessünk δ=min(δ 1 , δ2 } .Akkor a pont szomszédságában a sugár δ mindegyik egyenlőtlenség teljesülni fog |α(x)|< ε / 2 és | β(x)|< ε / 2. Ezért ezen a környéken lesz
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
azok. |f(x)|< ε, amit bizonyítani kellett.
2. tétel. Egy infinitezimális függvény szorzata fejsze) korlátozott funkcióhoz f(x) nál nél x→a(vagy mikor x→∞) egy végtelenül kicsi függvény.
Bizonyíték. Mivel a funkció f(x) korlátozott, akkor van egy szám M olyan, hogy minden értékre x egy pont valamelyik környékéről a|f(x)|≤M. Ráadásul mivel fejsze) egy végtelenül kicsi függvény at x→a, akkor tetszőleges ε-re > 0 van a pont szomszédsága a, amelyben az egyenlőtlenség érvényesül |α(x)|< ε /M. Aztán a kisebbik környéken van | αf|< ε /M= ε. Ez pedig azt jelenti af– végtelenül kicsi. Az alkalomra x→∞ a bizonyítást hasonlóan hajtják végre.
A bizonyított tételből az következik:
Következmény 1. Ha és akkor.
Következmény 2. Ha c= const, akkor .
3. tétel. Egy infinitezimális függvény aránya α(x) függvényenként f(x), amelynek határértéke eltér nullától, egy infinitezimális függvény.
Bizonyíték. Hadd ![]() . Aztán 1 /f(x) korlátozott funkciója van. Ezért a tört
. Aztán 1 /f(x) korlátozott funkciója van. Ezért a tört ![]() egy infinitezimális függvény és egy korlátos függvény szorzata, azaz. függvény végtelenül kicsi.
egy infinitezimális függvény és egy korlátos függvény szorzata, azaz. függvény végtelenül kicsi.
VÉGTELEN KICSI ÉS VÉGTELEN NAGY FUNKCIÓK KAPCSOLATA
1. tétel. Ha a funkció f(x) végtelenül nagy at x→a, majd az 1. függvény /f(x) végtelenül kicsi a x→a.
Bizonyíték. Vegyünk egy tetszőleges ε számot >0 és ezt mutasd meg egyeseknek δ>0 (ε-től függően) mindenre x, amelyekre |x – a|<δ , az egyenlőtlenség teljesül, és ez azt fogja jelenteni 1/f(x) egy végtelenül kicsi függvény. Valóban, azóta f(x) egy végtelenül nagy függvény at x→a, akkor lesz δ>0 olyan, hogy amint |x – a|<δ , tehát | f(x)|> 1/ ε. De akkor ugyanerre x.
Példák.
A fordított tétel is igazolható.
2. tétel. Ha a funkció f(x)- végtelenül kicsi x→a(vagy x→∞)és akkor nem tűnik el y= 1/f(x) egy végtelenül nagy függvény.
Végezze el saját maga a tétel bizonyítását.
Példák.
Így az infinitezimális és a végtelenül nagy függvények legegyszerűbb tulajdonságai a következő feltételes összefüggésekkel írhatók fel: A≠ 0
HATÁRTÉTELEK
1. tétel. Két, három és általában bizonyos számú függvény algebrai összegének határa megegyezik e függvények határainak algebrai összegével, azaz.
Bizonyíték. Végezzük el a bizonyítást két tagra, hiszen ugyanígy tetszőleges számú tagra elvégezhető. Hadd ![]() .Akkor f(x)=b+α(x)És g(x)=c+β(x), Ahol α
És β
– infinitezimális függvények. Ennélfogva,
.Akkor f(x)=b+α(x)És g(x)=c+β(x), Ahol α
És β
– infinitezimális függvények. Ennélfogva,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Mert b+c egy állandó és α(x) + β(x) akkor egy végtelenül kicsi függvény
Példa. .
2. tétel. Két, három és általában véges számú függvény szorzatának határa egyenlő ezen függvények határértékeinek szorzatával:
Bizonyíték. Hadd ![]() . Ennélfogva, f(x)=b+α(x)És g(x)=c+β(x)És
. Ennélfogva, f(x)=b+α(x)És g(x)=c+β(x)És
fg = (b + α) (c + β) = bc + (bβ + cα + αβ).
Munka időszámításunk előttállandó érték van. Funkció bβ + c α + αβ az infinitezimális függvények tulajdonságai alapján létezik egy infinitezimális mennyiség. Ezért .
Következmény 1. A konstans tényező a határjelen túlra vehető:
![]() .
.
Következmény 2. A fokhatár egyenlő a határfokkal:
![]() .
.
Példa.![]() .
.
3. tétel. Két függvény hányadosának határa egyenlő e függvények határértékeinek hányadosával, ha a nevező határértéke eltér nullától, azaz.
 .
.
Bizonyíték. Hadd . Ennélfogva, f(x)=b+α(x)És g(x)=c+β(x), Ahol α, β – végtelenül kicsi. Tekintsük a hányadost
A tört egy végtelenül kicsi függvény, mert a számláló egy végtelenül kicsi függvény, és a nevezőnek van határa c 2 ≠0.
Példák.

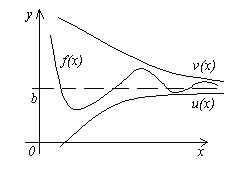
4. tétel. Legyen három függvény adott f(x), u(x)És v(x), az egyenlőtlenségek kielégítése u (x)≤f(x)≤ v(x). Ha a funkciók u(x)És v(x) ugyanaz a határérték x→a(vagy x→∞), majd a függvényt f(x) ugyanarra a határra hajlik, i.e. Ha
![]() , Azt .
, Azt .
Ennek a tételnek a jelentése világos az ábrából.
A 4. tétel bizonyítása megtalálható például a tankönyvben: Piskunov N. S. Differential and integral calculus, 1. kötet - M.: Nauka, 1985.
5. tétel.Én Kövér x→a(vagy x→∞) funkciót y=f(x) nem negatív értékeket fogad el y≥0és ugyanakkor a határra hajlik b, akkor ez a határ nem lehet negatív: b≥0.
Bizonyíték. Ellentmondásos bizonyítást fogunk végezni. Tegyünk úgy, mintha b<0 , Akkor |y – b|≥|b|és ezért a különbségi modulus nem nullázódik, amikor x→a. De aztán y nem éri el a határt b nál nél x→a, ami ellentmond a tétel feltételeinek.
6. tétel. Ha két funkciót f(x)És g(x) az érv összes értékére x kielégíti az egyenlőtlenséget f(x)≥ g(x)és vannak határai, akkor az egyenlőtlenség érvényes b≥c.
Bizonyíték. A tétel feltételei szerint f(x)-g(x) ≥0, ezért az 5. Tétel szerint ![]() , vagy
, vagy ![]() .
.
EGYOLDALÚ KORLÁTOK

Eddig fontolgattuk egy függvény határának meghatározását, amikor x→aönkényes módon, pl. a funkció határa nem attól függött, hogy hol helyezték el x felé a, balra vagy jobbra a. Azonban meglehetősen gyakori, hogy olyan függvényeket találunk, amelyeknek nincs korlátja ebben a feltételben, de van korlátjuk, ha x→a, az egyik oldalán maradva A, balra vagy jobbra (lásd az ábrát). Ezért bevezetjük az egyoldalú határok fogalmát.
Ha f(x) a határig hajlik b nál nél x egy bizonyos számra hajlamos aÍgy x csak a kisebb értékeket fogadja el a, akkor írnak és hívnak az f(x) függvény határértéke a bal oldali a pontban.
Infinitezimálisok és nagyok számítása
Infinitezimális számítás- infinitezimális mennyiségekkel végzett számítások, amelyekben a származtatott eredményt a végtelen kicsinyek végtelen összegének tekintjük. Az infinitezimálisok számítása a differenciál- és integrálszámítás általános fogalma, amely a modern felsőbb matematika alapját képezi. Az infinitezimális mennyiség fogalma szorosan összefügg a határ fogalmával.
Elenyésző
Utóbbi a n hívott elenyésző, Ha . Például egy számsorozat végtelenül kicsi.
A függvényt hívják végtelenül kicsi egy pont közelében x 0 ha ![]() .
.
A függvényt hívják végtelenül kicsi a végtelenben, Ha ![]() vagy
vagy ![]() .
.
Szintén infinitezimális az a függvény, amely a függvény és a határértéke közötti különbség, azaz ha ![]() , Azt f(x) − a = α( x)
, .
, Azt f(x) − a = α( x)
, .
Végtelenül nagy mennyiség
Utóbbi a n hívott végtelenül nagy, Ha ![]() .
.
A függvényt hívják végtelenül nagy egy pont közelében x 0 ha ![]() .
.
A függvényt hívják végtelenül nagy a végtelenben, Ha ![]() vagy
vagy ![]() .
.
Az egyenlőség jogának végtelensége minden esetben azt jelenti, hogy van egy bizonyos jel (vagy „plusz” vagy „mínusz”). Ez például a függvény x bűn x nem végtelenül nagy at .
A végtelenül kicsi és a végtelenül nagy tulajdonságai
Végtelenül kicsi mennyiségek összehasonlítása
Hogyan hasonlítsuk össze a végtelenül kicsi mennyiségeket?
Az infinitezimális mennyiségek aránya alkotja az úgynevezett bizonytalanságot.
Definíciók
Tegyük fel, hogy infinitezimális α( x) és β( x) (vagy ami a definíció szempontjából nem fontos, infinitezimális sorozatok).
Az ilyen határértékek kiszámításához célszerű a L'Hopital-szabályt használni.
Összehasonlítási példák
Használata RÓL RŐL-szimbolika, a kapott eredményeket a következő formában írhatjuk fel x 5 = o(x 3). Ebben az esetben a következő bejegyzések igazak: 2x 2 + 6x = O(x) És x = O(2x 2 + 6x).Egyenértékű értékek
Meghatározás
Ha , akkor az α és β végtelenül kicsiny mennyiségeket nevezzük egyenértékű ().
Nyilvánvaló, hogy az ekvivalens mennyiségek az azonos kicsinységi nagyságrendű végtelenül kicsi mennyiségek speciális esetét jelentik.
Ha a következő ekvivalencia viszonyok érvényesek: , , ![]() .
.
Tétel
Két végtelenül kicsi mennyiség hányadosának (arányának) határa nem változik, ha az egyiket (vagy mindkettőt) egy ekvivalens mennyiségre cseréljük.Ennek a tételnek gyakorlati jelentősége van a határok megtalálásakor (lásd a példát).
Használati példa
Csere sénn 2x egyenértékű érték 2 x, kapunkTörténelmi vázlat
Az „infinitezimális” fogalmát már az ókorban tárgyalták az oszthatatlan atomok fogalmával kapcsolatban, de a klasszikus matematikában nem szerepelt. A 16. században az „oszthatatlanok módszerének” megjelenésével újjáéledt – a vizsgált figurát végtelenül kis részekre osztva.
A 17. században megtörtént az infinitezimális számítás algebraizálása. Olyan numerikus mennyiségekként kezdték meghatározni őket, amelyek kisebbek bármely véges (nem nulla) mennyiségnél, és mégsem egyenlők nullával. Az elemzés művészete abból állt, hogy felállítottunk egy infinitezimálisokat (differenciálokat) tartalmazó relációt, majd integráltuk azt.
A régi iskola matematikusai próbára teszik a koncepciót elenyésző kemény kritika. Michel Rolle azt írta, hogy az új kalkulus: zseniális hibák halmaza"; Voltaire maróan megjegyezte, hogy a kalkulus olyan dolgok kiszámításának és pontos mérésének művészete, amelyek létezését nem lehet bizonyítani. Még Huygens is elismerte, hogy nem értette a magasabb rendű különbségek jelentését.
A Párizsi Tudományos Akadémián az elemzés indokoltságáról folyó viták olyan botrányossá váltak, hogy az Akadémia egyszer teljesen megtiltotta tagjainak, hogy ebben a témában felszólaljanak (ez főleg Rolle és Varignon volt). 1706-ban Rolle nyilvánosan visszavonta kifogásait, de a megbeszélések tovább folytatódtak.
1734-ben a híres angol filozófus, George Berkeley püspök kiadott egy szenzációs röpiratot, amely rövidített címmel ismert. Elemző" A teljes neve: " A hitetlen matematikushoz címzett elemző vagy diskurzus, amelyben azt kérdezik, hogy a modern elemzés tárgyát, alapelveit és következtetéseit világosabban érzékelik-e vagy világosabban levezetik-e, mint a vallási szentségeket és hittételeket.».
Az elemző szellemes és nagyrészt igazságos kritikát fogalmazott meg az infinitezimális számítással kapcsolatban. Berkeley úgy vélte, hogy az elemzési módszer nem egyeztethető össze a logikával, és ezt írta: bármennyire is hasznos, csak egyfajta találgatásnak tekinthető; ügyes ügyesség, művészet vagy inkább trükk, de nem tudományos bizonyítási módszerként" Idézve Newton mondatát a jelenlegi mennyiségek növekedéséről „keletkezésük vagy eltűnésük legelején”, Berkeley ironikusan: „ nem véges mennyiségek, nem is végtelenül kicsik, de még csak nem is semmik. Nem nevezhetnénk őket elhalt nagyságrendű kísérteteknek?... És hogyan beszélhetünk általánosságban olyan dolgok kapcsolatáról, amelyeknek nincs nagysága?.. Bárki, aki meg tudja emészteni a második vagy harmadik fluxust [származékot], a másodikat vagy a harmadikat különbséget, nem szabad, mivel úgy tűnik, hogy valami hibát találok a teológiában».
Lehetetlen – írja Berkeley – elképzelni a pillanatnyi sebességet, vagyis a sebességet egy adott pillanatban és egy adott pontban, mert a mozgás fogalmába beletartozik a (véges, nem nulla) tér és idő fogalma.
Hogyan ad helyes eredményt az elemzés? Berkeley arra a gondolatra jutott, hogy ezt az elemzési következtetések számos hibájával magyarázzák, és ezt egy parabola példájával illusztrálta. Érdekes, hogy néhány jelentős matematikus (például Lagrange) egyetértett vele.
Paradox helyzet állt elő, amikor a matematika szigora és termékenysége megzavarta egymást. Annak ellenére, hogy rosszul definiált fogalmakkal illegális akciókat alkalmaztak, a közvetlen hibák száma meglepően kicsi volt - az intuíció segített. Pedig a 18. század során a matematikai elemzés gyorsan fejlődött, lényegében minden indoklás nélkül. Hatékonysága elképesztő volt, és önmagáért beszélt, de a differenciálmű jelentése még mindig homályos volt. Különösen gyakran keverték össze egy függvény infinitezimális növekményét és annak lineáris részét.
A 18. század folyamán óriási erőfeszítések történtek a helyzet korrigálása érdekében, amelyekben a század legjobb matematikusai is részt vettek, de az elemzés alapjait csak Cauchynak sikerült meggyőzően felépítenie a 19. század elején. Szigorúan meghatározta az alapfogalmakat - határ, konvergencia, folytonosság, differenciál stb., ami után a tényleges infinitezimálisok eltűntek a tudományból. Néhány fennmaradó finomságot később ismertettünk
Tétel 2.4. Ha az (x n) és (y n) sorozatok konvergálnak, és x n ≤ y n, n > n 0, akkor lim x n ≤ lim y n.
Legyen lim xn = a, |
lim yn = b és a > b. Definíció szerint a 2.4 határértékek |
||||||||||||||||||||
sorozatok szám szerint ε = |
van egy olyan N szám |
||||||||||||||||||||
Ezért n > max(n0 , N) yn< |
< xn , что противоречит |
||||||||||||||||||||
feltétel. |
|||||||||||||||||||||
Megjegyzés. Ha az (xn), (yn) sorozatok konvergálnak |
|||||||||||||||||||||
mind n > n0 |
xn< yn , то можно утверждать лишь, что lim xn |
≤ lim yn . |
|||||||||||||||||||
Ennek belátásához elég figyelembe venni a sorozatokat
és yn = |
||||
A következő eredmények közvetlenül a 2.4 definícióból következnek.
Tétel 2.5. Ha az (x n) számsorozat konvergál és lim x n< b (b R), то N N: x n < b, n >N.
Következmény. Ha az (xn) sorozat konvergál és lim xn 6= 0, akkor
N N: sgn xn = sgn(lim xn), n > N.
Tétel 2.6. Az (x n), (y n), (z n) sorozatok teljesítsék a feltételeket:
1) x n ≤ yn ≤ zn , n > n0 ,
2) sorozatok(x n) és (z n) konvergál, és lim x n = lim z n = a.
Ekkor az (y n ) sorozat konvergál és lim y n = a.
2.1.3 Infinitezimális sorozatok
Meghatározás 2.7. Egy számsorozatot (x n) infinitezimálisnak (infinitezimálisnak) nevezünk, ha konvergál és lim x n = 0.
A számsorozat határértékének 2.4 definíciója szerint a 2.7 definíció a következővel egyenértékű:
Meghatározás 2.8. Egy (x n) számsorozatot végtelenül kicsinek nevezünk, ha bármely ε pozitív számhoz létezik olyan N = N(ε), hogy minden n > N esetén ennek a sorozatnak az x n elemei kielégítik az |x n |< ε.
Tehát (xn) - b.m. ε > 0 N = N(ε) : n > N |xn |< ε.
A 2., 3. példákból és a 2.3. tétel 1. megjegyzéséből azt kapjuk, hogy azután
érvényesség ( |
q−n |
végtelenek |
||||||||||||
Az infinitezimális sorozatok tulajdonságait a következő tételek írják le.
Tétel 2.7. Véges számú infinitezimális sorozat összege egy infinitezimális sorozat.
Legyenek az (xn), (yn) sorozatok végtelenül kicsik. Mutassuk meg, hogy (xn + yn) is egy lesz. Állítsuk be ε > 0-t. Ekkor van egy szám
N1 = N1 (ε) úgy, hogy |
||||
|xn |< |
N>N1, |
|||
és van olyan N2 = N2 (ε) szám, amelyre |
||||
|yn |< |
N>N2. |
|||
Jelöljük N = max(N1, N2). n > N esetén a (2.1) és (2.2) egyenlőtlenségek érvényesek. Ezért n > N esetén
|xn + yn | ≤ |xn | + |yn |< 2 + 2 = ε.
Ez azt jelenti, hogy az (xn +yn) sorozat végtelenül kicsi. Állítás véges számú infinitezimális sorozat összegéről
Ez az indukcióval igazoltakból következik.
Tétel 2.8. Egy infinitezimális sorozat és egy korlátos sorozat szorzata végtelenül kicsi.
Legyen (xn) korlátos és (yn) infinitezimális sorozat. A 2.6 definíció szerint egy korlátos sorozatnak van olyan M > 0 szám, amelyre
|xn | ≤ M, n N. |
Rögzítsünk egy tetszőleges ε > 0 számot. Mivel (yn) infinitezimális sorozat, létezik egy N = N(ε) szám,
Ezért a sorozat (xn yn ) végtelenül kicsi.

Következmény 1. Egy infinitezimális sorozat és egy konvergens sorozat szorzata egy infinitezimális sorozat.
Következmény 2. Két infinitezimális sorozat szorzata egy infinitezimális sorozat.
Infinitezimális sorozatokat használva a konvergens sorozat definíciója másképp nézhető meg.
Lemma 2.1. Ahhoz, hogy az a szám legyen az (x n) numerikus sorozat határa, szükséges és elegendő, hogy legyen egy x n = a + α n, n N reprezentáció, amelyben (α n) egy végtelenül kicsi sorozat.
Szükségesség. Legyen lim xn = a és a R. Ekkor
ε > 0 N = N(ε) N: n > N |xn − a|< ε.
Ha beállítjuk αn = xn − a, n N, akkor azt kapjuk, hogy (αn) egy infinitezimális sorozat és xn = a + αn, n N.
Megfelelőség. Legyen az (xn) sorozat olyan, hogy létezik olyan a szám, amelyre xn = a + αn, n N és lim αn = 0. Rögzítsünk egy tetszőleges ε pozitív számot. Mivel lim αn = 0, akkor létezik olyan N = N(ε) N szám, amelyre |αn |< ε, n >N. Vagyis más jelölésekben n > N |xn − a|< ε. Это означает, что lim xn = a.
Alkalmazzuk a 2.1 lemmát egy fontos konkrét példára.
Lemma 2.2. lim n n = 1.
√ √
Mivel minden n > 1 n n > 1 esetén n n = 1 + αn , és αn > 0
minden n > 1. Ezért n = (1 + α |
)n = 1 + nα |
+ αn. |
|||||||||||||||
Mivel minden tag pozitív, n |
|||||||||||||||||
Legyen ε > 0. Mivel |
2/n< ε для всех n >2/ε , akkor, feltételezve |
||||||||||||||||
N = max(1, ), azt kapjuk, hogy 0< αn < ε, n >N. Ezért
az (αn) sorozat infinitezimális és a lemma szerint
2,1, lim n n = 1. √
Következmény. Ha a > 1, akkor lim n a = 1.√ √
Az állítás az 1. egyenlőtlenségekből következik< n a ≤ n n , n >[a].
2.1.4 Aritmetikai műveletek sorozatokkal
A 2.1-es lemma és az infinitezimális sorozatok tulajdonságai segítségével könnyen tételeket kaphatunk a konvergens sorozatokból aritmetikai műveletekkel kapott sorozatok határértékeiről.

|b| 3|b|
2 < |y n | < 2
2.9. Tétel. Konvergáljanak az (x n) és (y n) számsorozatok. Akkor a következő állítások érvényesek:
1) a sorozat (x n ± y n ) konvergál és
lim(xn ± yn) = lim xn ± lim yn;
2) az (x n · y n ) sorozat konvergál és
lim(xn · yn ) = lim xn · lim yn ;
3) ha lim y n 6= 0, akkor az x n /y n arányt a következőtől kezdve határozzuk meg:
valamilyen szám, az ( x n ) sorozat konvergál és
A 2.8 Tétel és az 1. Következmény szerint az (a · βn), (b · αn), (αn · βn) sorozatok végtelenül kicsik. A 2.7. Tétel szerint a sorozat (aβn + bαn + αn βn ) végtelenül kicsi. A 2. állítás a 2.1. lemma (2.5) ábrázolásából következik.
Térjünk rá a 3) állításra. Feltétel szerint lim yn = b 6= 0. A 2.3. Tétel értelmében. a sorozat (|yn |) konvergál és lim |yn | = |b| 6= 0. Ezért az ε = |b|/2 szám mellett van egy N szám, amelyre n > N
0 < | 2 b| = |b| −
Ezért yn =6 0, és 3|b|< y n < |b| , n >N.
Így az xn /yn hányados minden n > N-re definiálva van, és az (1/yn) sorozat korlátozott. Tekintsük minden n > N esetén a különbséget
(αn b − aβn ). |
|||||||||||||||||||||
Utóbbi |
αn b |
aβn |
Végtelenül kicsi |
||||||||||||||||||
korlátozott. A 2.8 tétel szerint a sorozat |
|||||||||||||||||||||
− b |
|||||||||||||||||||||
nagyon kicsi. Ezért a 2.1 lemma a 3) állítást bizonyítja. Következmény 1. Ha az (xn) sorozat konvergál, akkor bármelyikre
Bármely c szám esetén a (c · xn ) sorozat konvergál, és lim(cxn ) = c · lim xn .
Infinitezimális függvények
A %%f(x)%% függvény meghívásra kerül elenyésző(b.m.) %%x \to a \in \overline(\mathbb(R))%%, ha az argumentum ezen tendenciájával a függvény határértéke nulla.
A b.m. fogalma. A függvény elválaszthatatlanul kapcsolódik az argumentumát módosító utasításokhoz. Beszélhetünk a b.m. függvények: %%a \to a + 0%% és %%a \to a - 0%%. Általában b.m. a függvényeket a görög ábécé első betűivel jelöljük %%\alpha, \beta, \gamma, \ldots%%
Példák
- A %%f(x) = x%% függvény a b.m. %%x \to 0%%, mivel a határa a %%a = 0%% pontban nulla. A kétoldali határ és az egyoldali határ kapcsolatáról szóló tétel szerint ez a függvény b.m. mind a %%x \to +0%% és a %%x \to -0%% értékkel.
- Függvény %%f(x) = 1/(x^2)%% - b.m. %%x \to \infty%% között (valamint %%x \to +\infty%% és %%x \to -\infty%%) között.
Egy nem nulla állandó szám, bármilyen kicsi is abszolút értékben, nem b.m. funkció. Állandó számok esetén az egyetlen kivétel a nulla, mivel a %%f(x) \equiv 0%% függvény nulla határértékkel rendelkezik.
Tétel
A %%f(x)%% függvénynek a kiterjesztett számsor %%a \in \overline(\mathbb(R))%% pontjában van egy végső korlátja, amely akkor és csak a %%b%% számmal egyenlő ha ez a függvény egyenlő ennek a számnak a %%b%% és a b.m összegével. %%\alpha(x)%% függvények %%x \to a%%, vagy $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Baljobbra nyíl \bal(f(x) = b + \alpha(x)\jobbra) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\jobbra). $$
Infinitezimális függvények tulajdonságai
A %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, határértékre való áthaladás szabályai szerint a következő állítások következnek:
- A végső szám összege a b.m. függvények %%x-hez \to a%% a b.m. itt: %%x \to a%%.
- Bármely szám szorzata b.m. függvények %%x-hez \to a%% a b.m. itt: %%x \to a%%.
Termék b.m. függvények %%x \to a%% pontban, és egy függvény, amely az a pont %%\stackrel(\circ)(\text(U))(a)%% pontjában van átszúrva, ott van b.m. a %%x \to a%% függvényben.
Nyilvánvaló, hogy egy állandó függvény és a b.m szorzata. %%x \to a%% között van b.m. függvény: %%x \to a%%.
Egyenértékű infinitezimális függvények
A %%\alpha(x), \beta(x)%% végtelen kicsi függvények a %%x \to a%% esetén egyenértékűés írja be a %%\alpha(x) \sim \beta(x)%%, ha
$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alpha(x))) = 1. $$
Tétel a b.m pótlásáról. funkciók egyenértékűek
Legyen %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% b.m. függvények %%x \to a%%, %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, majd $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ limits_(x \to a)(\frac(\alpha_1(x))(\beta_1(x))). $$
Egyenértékű b.m. funkciókat.
Legyen %%\alpha(x)%% b.m. függvény %%x \to a%%, akkor
- %%\sin(\alpha(x)) \sim \alpha(x)%%
- %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
- %%\tan \alpha(x) \sim \alpha(x)%%
- %%\arcsin\alpha(x) \sim \alpha(x)%%
- %%\arctan\alpha(x) \sim \alpha(x)%%
- %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
- %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
- %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%
Példa
$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(tömb) $$
Végtelenül nagy funkciók
A %%f(x)%% függvény meghívásra kerül végtelenül nagy(b.b.) %%x \to a \in \overline(\mathbb(R))%%, ha az argumentum ezen tendenciájával a függvénynek végtelen határa van.
Hasonló a b.m. függvények fogalma b.b. A függvény elválaszthatatlanul kapcsolódik az argumentumát módosító utasításokhoz. Beszélhetünk a b.b. függvények: %%x \to a + 0%% és %%x \to a - 0%%. A „végtelenül nagy” kifejezés nem a függvény abszolút értékéről, hanem a kérdéses pont környezetében bekövetkezett változásának természetéről beszél. Egyetlen állandó szám sem, akármekkora is legyen abszolút értékben, végtelenül nagy.
Példák
- %%f(x) = 1/x%% függvény - b.b. %%x \-0%% között.
- Függvény %%f(x) = x%% - b.b. %%x \to \infty%%.
Ha a definíciós feltételek $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(tömb) $$
aztán arról beszélnek pozitív vagy negatív b.b. %%a%% függvénynél.
Példa
%%1/(x^2)%% függvény - pozitív b.b. %%x \-0%% között.
A kapcsolat a b.b. és b.m. funkciókat
Ha %%f(x)%% b.b. %%x \to a%% függvénnyel, majd %%1/f(x)%% - b.m.
itt: %%x \to a%%. Ha %%\alpha(x)%% - b.m. mert %%x \to a%% egy nem nulla függvény a %%a%% pont valamely átszúrt környezetében, akkor a %%1/\alpha(x)%% b.b. itt: %%x \to a%%.
Végtelenül nagy függvények tulajdonságai
Mutassuk be a b.b. számos tulajdonságát. funkciókat. Ezek a tulajdonságok közvetlenül a b.b definíciójából következnek. véges határértékekkel rendelkező függvények függvényei és tulajdonságai, valamint a b.b. közötti kapcsolatra vonatkozó tételből. és b.m. funkciókat.
- Egy véges számú b.b szorzata. függvények %%x \to a%% számára b.b. függvény: %%x \to a%%. Valóban, ha %%f_k(x), k = \overline(1, n)%% - b.b. függvények: %%x \to a%%, majd a %%a%% %%f_k(x) \ne 0%% pont valamilyen kilyukasztott környezetében, és kapcsolódási tétel alapján b.b. és b.m. függvények %%1/f_k(x)%% - b.m. függvény: %%x \to a%%. Kiderült, hogy %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m függvény %%x \to a%%, és %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. függvény: %%x \to a%%.
- Termék b.b. függvények %%x \to a%%-ra, és egy olyan függvény, amely a %%a%% pont valamely kiszúrt környezetében abszolút értékben nagyobb, mint egy pozitív állandó, b.b. függvény: %%x \to a%%. Különösen a termék b.b. egy %%x \to a%% függvény és egy véges, nem nulla határértékkel rendelkező függvény a %%a%% pontban b.b. függvény: %%x \to a%%.
Két b.b. függvények %%x \to a%% között bizonytalanság van. A feltételek előjelétől függően egy ilyen összeg változásának jellege nagyon eltérő lehet.
Példa
Legyenek adottak a %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%% függvények. függvények: %%x \to \infty%%. Akkor:
- %%f(x) + g(x) = 3x%% - b.b. függvény: %%x \to \infty%%;
- %%f(x) + h(x) = 0%% - b.m. függvény: %%x \to \infty%%;
- %%h(x) + v(x) = \sin x%% nincs korlátja %%x \to \infty%%.
A %%a%% pont és a b.b pont valamely átszúrt környezetében határolt függvény összege. függvények %%x-el \to a%% a b.b. függvény: %%x \to a%%.
Például a %%x - \sin x%% és a %%x + \cos x%% függvények b.b. %%x \to \infty%%.
