Successioni infinitesime – definizione e proprietà. Esempi Quale quantità è chiamata infinitesima
Calcolo degli infinitesimi e dei grandi
Calcolo infinitesimale- calcoli eseguiti con quantità infinitesime, in cui il risultato derivato è considerato come una somma infinita di infinitesimi. Il calcolo degli infinitesimi è un concetto generale del calcolo differenziale e integrale, che costituisce la base della matematica superiore moderna. Il concetto di quantità infinitesima è strettamente correlato al concetto di limite.
Infinitesimale
Sotto sequenza UN N chiamato infinitesimale, Se . Ad esempio, una sequenza di numeri è infinitesima.
La funzione viene chiamata infinitesimo in prossimità di un punto X 0 se ![]() .
.
La funzione viene chiamata infinitesimo all'infinito, Se ![]() O
O ![]() .
.
Anche infinitesimale è una funzione che è la differenza tra una funzione e il suo limite, cioè se ![]() , Quello F(X) − UN = α( X)
, .
, Quello F(X) − UN = α( X)
, .
Quantità infinitamente grande
In tutte le formule seguenti, è implicito che l'infinito a destra dell'uguaglianza abbia un certo segno ("più" o "meno"). Questa è, ad esempio, la funzione X peccato X, illimitato su entrambi i lati, non è infinitamente grande in .
Sotto sequenza UN N chiamato infinitamente grande, Se ![]() .
.
La funzione viene chiamata infinitamente grande in prossimità di un punto X 0 se ![]() .
.
La funzione viene chiamata infinitamente grande all'infinito, Se ![]() O
O ![]() .
.
Proprietà dell'infinitamente piccolo e dell'infinitamente grande
Confronto di quantità infinitesime
Come confrontare quantità infinitesimali?
Il rapporto tra quantità infinitesimali costituisce la cosiddetta incertezza.
Definizioni
Supponiamo di avere valori infinitesimi α( X) e β( X) (o, cosa non importante ai fini della definizione, successioni infinitesimali).
Per calcolare tali limiti è conveniente utilizzare la regola di L'Hopital.
Esempi di confronto
Utilizzando DI-simbolismo, i risultati ottenuti possono essere scritti nella forma seguente X 5 = o(X 3). In questo caso sono vere le seguenti voci: 2X 2 + 6X = O(X) E X = O(2X 2 + 6X).Valori equivalenti
Definizione
Se , allora si chiamano le quantità infinitesime α e β equivalente ().
È ovvio che le quantità equivalenti sono un caso speciale di quantità infinitesime dello stesso ordine di piccolezza.
Quando valgono le seguenti relazioni di equivalenza (come conseguenza dei cosiddetti limiti notevoli):
Teorema
Il limite del quoziente (rapporto) di due quantità infinitesime non cambierà se una di esse (o entrambe) viene sostituita da una quantità equivalente.Questo teorema ha un significato pratico quando si trovano i limiti (vedi esempio).
Esempio di utilizzo
Sostituzione SioN 2X valore equivalente 2 X, noi abbiamoSchizzo storico
Il concetto di “infinitesimale” veniva discusso già nell’antichità in relazione al concetto di atomi indivisibili, ma non era incluso nella matematica classica. Fu ripreso nuovamente con l'avvento nel XVI secolo del “metodo degli indivisibili” che divideva la figura oggetto di studio in sezioni infinitesimali.
Nel XVII secolo ebbe luogo l'algebrizzazione del calcolo infinitesimale. Cominciarono a essere definiti come quantità numeriche inferiori a qualsiasi quantità finita (diversa da zero) e tuttavia non uguali a zero. L'arte dell'analisi consisteva nel tracciare una relazione contenente degli infinitesimi (differenziali) e poi nell'integrarla.
I matematici della vecchia scuola mettono alla prova il concetto infinitesimale dura critica. Michel Rolle ha scritto che il nuovo calcolo è “ insieme di errori ingegnosi"; Voltaire osservò causticamente che il calcolo infinitesimale è l'arte di calcolare e misurare accuratamente cose la cui esistenza non può essere dimostrata. Perfino Huygens ammise di non comprendere il significato dei differenziali di ordine superiore.
Come ironia del destino, si può considerare l'emergere, a metà del secolo, dell'analisi non standard, che ha dimostrato che anche il punto di vista originale - gli infinitesimi reali - era coerente e poteva essere utilizzato come base per l'analisi.
Guarda anche
Fondazione Wikimedia. 2010.
Scopri cos'è la "quantità infinitesimale" in altri dizionari:
QUANTITÀ INFINITAMENTE PICCOLA- una quantità variabile in un certo processo, se in questo processo si avvicina (tende) infinitamente a zero... Grande Enciclopedia del Politecnico
Infinitesimale- ■ Qualcosa di sconosciuto, ma legato all'omeopatia... Lessico delle verità comuni
INFINITE PICCOLE FUNZIONI E LORO PROPRIETÀ FONDAMENTALI
Funzione y=f(x) chiamato infinitesimale A x→a o quando X→∞, se o , cioè una funzione infinitesima è una funzione il cui limite in un dato punto è zero.
Esempi.
Stabiliamo la seguente importante relazione:
Teorema. Se la funzione y=f(x) rappresentabile con x→a come somma di un numero costante B e grandezza infinitesimale α(x): f(x)=b+ α(x) Quello .
Viceversa, se , allora f(x)=b+α(x), Dove ascia)– infinitesimo a x→a.
Prova.
Consideriamo le proprietà di base delle funzioni infinitesime.
Teorema 1. La somma algebrica di due, tre e in generale di qualsiasi numero finito di infinitesimi è una funzione infinitesima.
Prova. Diamo una dimostrazione per due termini. Permettere f(x)=α(x)+β(x), dove e . Dobbiamo dimostrarlo per ogni piccolo ε arbitrario > 0 trovato δ> 0, tale che per X, soddisfacendo la disuguaglianza |x – a|<δ , eseguita |f(x)|< ε.
Quindi, fissiamo un numero arbitrario ε > 0. Poiché secondo le condizioni del teorema α(x)è una funzione infinitesima, allora esiste tale δ 1 > 0, ovvero |x – a|< δ 1 abbiamo |α(x)|< ε / 2. Allo stesso modo, da allora β(x)è infinitesimo, allora esiste tale δ 2 > 0, ovvero |x – a|< δ 2 abbiamo | β(x)|< ε / 2.
Prendiamo δ=min(δ1 , δ2 } .Quindi in prossimità del punto UN raggio δ ciascuna delle disuguaglianze sarà soddisfatta |α(x)|< ε / 2 e | β(x)|< ε / 2. Pertanto, in questo quartiere ci sarà
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
quelli. |f(x)|< ε, che è ciò che doveva essere dimostrato.
Teorema 2. Prodotto di una funzione infinitesima ascia) per una funzione limitata f(x) A x→a(o quando x→∞) è una funzione infinitesima.
Prova. Poiché la funzione f(x)è limitato, quindi c'è un numero M tale che per tutti i valori X da qualche intorno di un punto a|f(x)|≤M. Inoltre, da allora ascia)è una funzione infinitesima a x→a, quindi per un ε arbitrario > 0 c'è un intorno del punto UN, in cui vale la disuguaglianza |α(x)|< ε /M. Poi nel più piccolo di questi quartieri abbiamo | αf|< ε /M= ε. E questo significa questo af– infinitesimo. Per l'occasione x→∞ la dimostrazione si svolge in modo simile.
Dal teorema dimostrato segue:
Corollario 1. Se e, allora.
Corollario 2. Se c= const, quindi .
Teorema 3. Rapporto di una funzione infinitesima α(x) per funzione f(x), il cui limite è diverso da zero, è una funzione infinitesimale.
Prova. Permettere ![]() . Quindi 1 /f(x) c'è una funzione limitata. Quindi la frazione
. Quindi 1 /f(x) c'è una funzione limitata. Quindi la frazione ![]() è il prodotto di una funzione infinitesima e di una funzione limitata, cioè la funzione è infinitesimale.
è il prodotto di una funzione infinitesima e di una funzione limitata, cioè la funzione è infinitesimale.
RAPPORTO TRA FUNZIONI INFINITAMENTE PICCOLE E INFINITAMENTE GRANDI
Teorema 1. Se la funzione f(x)è infinitamente grande a x→a, quindi funzione 1 /f(x)è infinitesimale a x→a.
Prova. Prendiamo un numero arbitrario ε >0 e dimostrarlo per alcuni δ>0 (a seconda di ε) per tutti X, per cui |x – a|<δ , la disuguaglianza è soddisfatta, e questo significherà questo 1/f(x)è una funzione infinitesima. Infatti, da allora f(x)è una funzione infinitamente grande in x→a, allora ci sarà δ>0 tale che non appena |x – a|<δ , quindi | f(x)|> 1/ ε. Ma poi per lo stesso X.
Esempi.
Si può dimostrare anche il teorema inverso.
Teorema 2. Se la funzione f(x)- infinitesimo a x→a(O x→∞) e non svanisce, quindi y= 1/f(x)è una funzione infinitamente grande.
Esegui tu stesso la dimostrazione del teorema.
Esempi.
Pertanto, le proprietà più semplici delle funzioni infinitesime e infinitamente grandi possono essere scritte utilizzando le seguenti relazioni condizionali: UN≠ 0
TEOREMI LIMITE
Teorema 1. Il limite della somma algebrica di due, tre e generalmente un certo numero di funzioni è uguale alla somma algebrica dei limiti di queste funzioni, cioè
Prova. Effettuiamo la dimostrazione per due termini, poiché si può fare allo stesso modo per qualsiasi numero di termini. Permettere ![]() .Poi f(x)=b+α(x) E g(x)=c+β(x), Dove α
E β
– funzioni infinitesime. Quindi,
.Poi f(x)=b+α(x) E g(x)=c+β(x), Dove α
E β
– funzioni infinitesime. Quindi,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Perché b+cè una costante e α(x) + β(x)è una funzione infinitesima, quindi
Esempio. .
Teorema 2. Il limite del prodotto di due, tre e generalmente un numero finito di funzioni è uguale al prodotto dei limiti di queste funzioni:
Prova. Permettere ![]() . Quindi, f(x)=b+α(x) E g(x)=c+β(x) E
. Quindi, f(x)=b+α(x) E g(x)=c+β(x) E
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Lavoro avanti Cristo c'è un valore costante. Funzione bβ + cα + αβ in base alle proprietà delle funzioni infinitesime, esiste una quantità infinitesima. Ecco perché .
Corollario 1. Il fattore costante può essere portato oltre il segno limite:
![]() .
.
Corollario 2. Il grado limite è uguale al grado limite:
![]() .
.
Esempio.![]() .
.
Teorema 3. Il limite del quoziente di due funzioni è uguale al quoziente dei limiti di queste funzioni se il limite del denominatore è diverso da zero, cioè
 .
.
Prova. Permettere . Quindi, f(x)=b+α(x) E g(x)=c+β(x), Dove α, β – infinitesimo. Consideriamo il quoziente
Una frazione è una funzione infinitesima perché il numeratore è una funzione infinitesima e il denominatore ha un limite c2≠0.
Esempi.

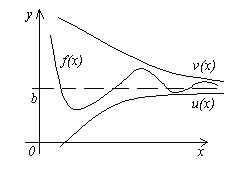
Teorema 4. Siano date tre funzioni f(x), u(x) E v(x), soddisfacendo le disuguaglianze u (x)≤f(x)≤ v(x). Se le funzioni u(x) E v(x) hanno lo stesso limite a x→a(O x→∞), quindi la funzione f(x) tende allo stesso limite, cioè Se
![]() , Quello .
, Quello .
Il significato di questo teorema è chiaro dalla figura.
La dimostrazione del Teorema 4 si trova, ad esempio, nel libro di testo: Piskunov N. S. Calcolo differenziale e integrale, vol 1 - M.: Nauka, 1985.
Teorema 5. Se a x→a(O x→∞) funzione y=f(x) accetta valori non negativi y≥0 e allo stesso tempo tende al limite B, allora questo limite non può essere negativo: b≥0.
Prova. Effettueremo la dimostrazione per assurdo. Facciamo finta che B<0 , Poi |y – b|≥|b| e, quindi, il modulo differenziale non tende a zero quando x→a. Ma allora sì non raggiunge il limite B A x→a, il che contraddice le condizioni del teorema.
Teorema 6. Se due funzioni f(x) E g(x) per tutti i valori dell'argomento X soddisfare la disuguaglianza f(x)≥ g(x) e hanno dei limiti, allora vale la disuguaglianza b≥c.
Prova. Secondo le condizioni del teorema f(x)-g(x) ≥0, quindi, dal Teorema 5 ![]() , O
, O ![]() .
.
LIMITI UNILATERALI

Finora abbiamo considerato la determinazione del limite di una funzione quando x→a in modo arbitrario, cioè il limite della funzione non dipendeva da come era posizionata X in direzione UN, a sinistra o a destra di UN. Tuttavia, è abbastanza comune trovare funzioni che non hanno limiti in questa condizione, ma hanno un limite se x→a, rimanendo su un lato di UN, sinistra o destra (vedi figura). Pertanto, vengono introdotti i concetti di limiti unilaterali.
Se f(x) tende al limite B A X tendente ad un certo numero UN COSÌ X accetta solo valori inferiori a UN, poi scrivono e chiamano blimite della funzione f(x) nel punto a a sinistra.
Calcolo degli infinitesimi e dei grandi
Calcolo infinitesimale- calcoli eseguiti con quantità infinitesime, in cui il risultato derivato è considerato come una somma infinita di infinitesimi. Il calcolo degli infinitesimi è un concetto generale del calcolo differenziale e integrale, che costituisce la base della matematica superiore moderna. Il concetto di quantità infinitesima è strettamente correlato al concetto di limite.
Infinitesimale
Sotto sequenza UN N chiamato infinitesimale, Se . Ad esempio, una sequenza di numeri è infinitesima.
La funzione viene chiamata infinitesimo in prossimità di un punto X 0 se ![]() .
.
La funzione viene chiamata infinitesimo all'infinito, Se ![]() O
O ![]() .
.
Anche infinitesimale è una funzione che è la differenza tra una funzione e il suo limite, cioè se ![]() , Quello F(X) − UN = α( X)
, .
, Quello F(X) − UN = α( X)
, .
Quantità infinitamente grande
Sotto sequenza UN N chiamato infinitamente grande, Se ![]() .
.
La funzione viene chiamata infinitamente grande in prossimità di un punto X 0 se ![]() .
.
La funzione viene chiamata infinitamente grande all'infinito, Se ![]() O
O ![]() .
.
In tutti i casi, è implicito che l'infinito a destra dell'uguaglianza abbia un certo segno ("più" o "meno"). Questa è, ad esempio, la funzione X peccato X non è infinitamente grande in .
Proprietà dell'infinitamente piccolo e dell'infinitamente grande
Confronto di quantità infinitesime
Come confrontare quantità infinitesimali?
Il rapporto tra quantità infinitesimali costituisce la cosiddetta incertezza.
Definizioni
Supponiamo di avere valori infinitesimi α( X) e β( X) (o, cosa non importante ai fini della definizione, successioni infinitesimali).
Per calcolare tali limiti è conveniente utilizzare la regola di L'Hopital.
Esempi di confronto
Utilizzando DI-simbolismo, i risultati ottenuti possono essere scritti nella forma seguente X 5 = o(X 3). In questo caso sono vere le seguenti voci: 2X 2 + 6X = O(X) E X = O(2X 2 + 6X).Valori equivalenti
Definizione
Se , allora si chiamano le quantità infinitesime α e β equivalente ().
È ovvio che le quantità equivalenti sono un caso speciale di quantità infinitesime dello stesso ordine di piccolezza.
Quando valgono le seguenti relazioni di equivalenza: , , ![]() .
.
Teorema
Il limite del quoziente (rapporto) di due quantità infinitesime non cambierà se una di esse (o entrambe) viene sostituita da una quantità equivalente.Questo teorema ha un significato pratico quando si trovano i limiti (vedi esempio).
Esempio di utilizzo
Sostituzione SioN 2X valore equivalente 2 X, noi abbiamoSchizzo storico
Il concetto di “infinitesimale” veniva discusso già nell’antichità in relazione al concetto di atomi indivisibili, ma non era incluso nella matematica classica. Fu ripreso nuovamente con l'avvento nel XVI secolo del “metodo degli indivisibili” che divideva la figura oggetto di studio in sezioni infinitesimali.
Nel XVII secolo ebbe luogo l'algebrizzazione del calcolo infinitesimale. Cominciarono a essere definiti come quantità numeriche inferiori a qualsiasi quantità finita (diversa da zero) e tuttavia non uguali a zero. L'arte dell'analisi consisteva nel tracciare una relazione contenente degli infinitesimi (differenziali) e poi nell'integrarla.
I matematici della vecchia scuola mettono alla prova il concetto infinitesimale dura critica. Michel Rolle ha scritto che il nuovo calcolo è “ insieme di errori ingegnosi"; Voltaire osservò causticamente che il calcolo infinitesimale è l'arte di calcolare e misurare accuratamente cose la cui esistenza non può essere dimostrata. Perfino Huygens ammise di non comprendere il significato dei differenziali di ordine superiore.
Le controversie all'Accademia delle Scienze di Parigi sulla giustificazione dell'analisi divennero così scandalose che l'Accademia una volta proibì completamente ai suoi membri di parlare su questo argomento (questo riguardava principalmente Rolle e Varignon). Nel 1706 Rolle ritirò pubblicamente le sue obiezioni, ma le discussioni continuarono.
Nel 1734, il famoso filosofo inglese, il vescovo George Berkeley, pubblicò un opuscolo sensazionale, noto con il titolo abbreviato “ Analista" Il suo nome completo: " Analista o discorso rivolto al matematico non credente, in cui si chiede se l'argomento, i principi e le conclusioni dell'analisi moderna siano percepiti o dedotti più chiaramente dei sacramenti religiosi e degli articoli di fede».
L'Analyst ha presentato una critica spiritosa e in gran parte giusta al calcolo infinitesimale. Berkeley considerò il metodo di analisi incoerente con la logica e scrisse che: “ per quanto utile possa essere, può essere considerata solo come una sorta di ipotesi; abilità abile, arte o meglio trucco, ma non come metodo di prova scientifica" Citando la frase di Newton sull’incremento delle quantità attuali “all’inizio della loro origine o scomparsa”, Berkeley ironizza: “ non sono né quantità finite, né infinitesimi, e nemmeno nulla. Non potremmo chiamarli fantasmi di grandezze defunte?... E come si può parlare in generale del rapporto tra cose che non hanno grandezza?... Chiunque sappia digerire la seconda o la terza flussione [derivata], la seconda o la terza differenza, non dovrebbe, poiché mi sembra trovare da ridire su qualcosa in teologia».
È impossibile, scrive Berkeley, immaginare la velocità istantanea, cioè la velocità in un dato istante e in un dato punto, perché il concetto di movimento comprende i concetti di spazio e tempo (finito non nullo).
In che modo l'analisi produce risultati corretti? Berkeley arrivò all'idea che ciò fosse spiegato dalla presenza di diversi errori nelle conclusioni analitiche e lo illustrò con l'esempio di una parabola. È interessante notare che alcuni importanti matematici (ad esempio Lagrange) erano d'accordo con lui.
Si è verificata una situazione paradossale quando il rigore e la fecondità in matematica hanno interferito a vicenda. Nonostante l'uso di azioni illegali con concetti poco definiti, il numero di errori diretti è stato sorprendentemente piccolo: l'intuizione è venuta in soccorso. Eppure, nel corso del XVIII secolo, l’analisi matematica si sviluppò rapidamente, sostanzialmente senza alcuna giustificazione. La sua efficienza era sorprendente e parlava da sola, ma il significato del differenziale non era ancora chiaro. Soprattutto l'incremento infinitesimale di una funzione e la sua parte lineare venivano spesso confusi.
Per tutto il XVIII secolo furono compiuti enormi sforzi per correggere la situazione e vi parteciparono i migliori matematici del secolo, ma solo Cauchy riuscì a costruire in modo convincente le basi dell'analisi all'inizio del XIX secolo. Ha definito rigorosamente i concetti di base: limite, convergenza, continuità, differenziale, ecc., Dopo di che gli infinitesimi reali sono scomparsi dalla scienza. Alcune sottigliezze rimanenti sono state spiegate in seguito
Teorema 2.4. Se le successioni (x n) e (y n) convergono e x n ≤ y n, n > n 0, allora lim x n ≤ lim y n.
Sia lim xn = a, |
lim yn = b e a > b. Per definizione 2.4 limiti |
||||||||||||||||||||
sequenze per numero ε = |
esiste un numero N tale che |
||||||||||||||||||||
Pertanto, n > max(n0 , N) yn< |
< xn , что противоречит |
||||||||||||||||||||
condizione. |
|||||||||||||||||||||
Commento. Se le successioni (xn), (yn) convergono per |
|||||||||||||||||||||
tutti n > n0 |
xnn< yn , то можно утверждать лишь, что lim xn |
≤ lim yn . |
|||||||||||||||||||
Per capirlo basta considerare le sequenze
e yn = |
||||
I seguenti risultati seguono direttamente dalla Definizione 2.4.
Teorema 2.5. Se la sequenza numerica (x n) converge e lim x n< b (b R), то N N: x n < b, n >N.
Conseguenza. Se la successione (xn) converge e lim xn 6= 0, allora
N N: sgn xn = sgn(lim xn), n > N.
Teorema 2.6. Poniamo che le successioni (x n), (y n), (z n) soddisfino le condizioni:
1) x n ≤ yn ≤ zn , n > n0 ,
2) sequenze(x n) e (z n) convergono e lim x n = lim z n = a.
Allora la successione (y n ) converge e lim y n = a.
2.1.3 Sequenze infinitesimali
Definizione 2.7. Una successione numerica (x n) si dice infinitesima (infinitesimale) se converge e lim x n = 0.
Secondo la Definizione 2.4 del limite di una sequenza numerica, la Definizione 2.7 è equivalente alla seguente:
Definizione 2.8. Una sequenza numerica (x n) si dice infinitesima se per ogni numero positivo ε esiste un numero N = N(ε) tale che per ogni n > N gli elementi x n di questa sequenza soddisfano la disuguaglianza |x n |< ε.
Quindi, (xn) - b.m. ε > 0 N = N(ε) : n > N |xn |< ε.
Dagli Esempi 2, 3 e dall'Osservazione 1 al Teorema 2.3 otteniamo ciò che segue
validità ( |
q−n |
sono infiniti |
||||||||||||
Le proprietà delle successioni infinitesime sono descritte dai seguenti teoremi.
Teorema 2.7. La somma di un numero finito di sequenze infinitesimali è una sequenza infinitesima.
Siano infinitesimali le successioni (xn), (yn). Mostriamo che anche (xn + yn) sarà uno. Poniamo ε > 0. Allora c'è un numero
N1 = N1 (ε) tale che |
||||
|xn |< |
N>N1, |
|||
ed esiste un numero N2 = N2 (ε) tale che |
||||
|yn |< |
N>N2. |
|||
Indichiamo con N = max(N1, N2). Per n > N varranno le disuguaglianze (2.1) e (2.2). Pertanto, per n > N
|xn + yn | ≤ |xn | + |yn |< 2 + 2 = ε.
Ciò significa che la successione (xn +yn) è infinitesima. Enunciato sulla somma di un numero finito di successioni infinitesime
Ciò segue da quanto dimostrato per induzione.
Teorema 2.8. Il prodotto di una successione infinitesima e di una successione limitata è infinitesimale.
Sia (xn) una successione limitata e (yn) una successione infinitesimale. Per la Definizione 2.6 di una successione limitata esiste un numero M > 0 tale che
|xn | ≤ M, nN. |
Fissiamo un numero arbitrario ε > 0. Poiché (yn) è una successione infinitesima, esiste un numero N = N(ε) tale che
Pertanto la sequenza (xn yn ) è infinitesimale.

Corollario 1. Il prodotto di una successione infinitesima e di una successione convergente è una successione infinitesima.
Corollario 2. Il prodotto di due successioni infinitesime è una successione infinitesima.
Utilizzando successioni infinitesime, la definizione di successione convergente può essere vista in modo diverso.
Lemma 2.1. Affinché il numero a sia limite della successione numerica (x n), è necessario e sufficiente che esista una rappresentazione x n = a + α n, n N, in cui (α n) è una successione infinitesimale.
Necessità. Sia lim xn = a e a R. Allora
ε > 0 N = N(ε) N: n > N |xn − a|< ε.
Se poniamo αn = xn − a, n N, allora otteniamo che (αn) è una successione infinitesima e xn = a + αn, n N.
Adeguatezza. Sia la successione (xn) tale che esista un numero a per il quale xn = a + αn, n N e lim αn = 0. Fissiamo un numero positivo arbitrario ε. Poiché lim αn = 0, allora esiste un numero N = N(ε) N tale che |αn |< ε, n >N. Cioè, in altre notazioni, n > N |xn − a|< ε. Это означает, что lim xn = a.
Applichiamo il Lemma 2.1 ad un importante esempio particolare.
Lemma 2.2. lim n n = 1.
√ √
Poiché per tutti n > 1 n n > 1, allora n n = 1 + αn , e αn > 0 per
tutto n > 1. Pertanto n = (1 + α |
)n = 1 + nα |
+αn. |
|||||||||||||||
Poiché tutti i termini sono positivi, n |
|||||||||||||||||
Sia ε > 0. Da allora |
2/n< ε для всех n >2/ε , quindi, assumendo |
||||||||||||||||
N = max(1, ), otteniamo 0< αn < ε, n >N. Pertanto,
la successione (αn) è infinitesima e, secondo il lemma
2.1, lim n n = 1. √
Conseguenza. Se a > 1, allora lim n a = 1.√ √
L’affermazione segue dalle disuguaglianze 1< n a ≤ n n , n >[UN].
2.1.4 Operazioni aritmetiche con sequenze
Utilizzando il Lemma 2.1 e le proprietà delle successioni infinitesime è facile ottenere teoremi sui limiti delle successioni ottenute mediante operazioni aritmetiche da successioni convergenti.

|b| 3|b|
2 < |y n | < 2
Teorema 2.9. Lascia che le sequenze numeriche (x n) e (y n) convergano. Allora valgono le seguenti affermazioni:
1) la successione (x n ± y n ) converge e
lim(xn ± yn) = lim xn ± lim yn;
2) la successione (x n · y n ) converge e
lim(xn · yn ) = lim xn · lim yn ;
3) se lim y n 6= 0, allora il rapporto x n /y n è definito a partire da
qualche numero, la successione ( x n ) converge e
Per il Teorema 2.8 e il Corollario 1, le successioni (a · βn), (b · αn), (αn · βn) sono infinitesime. Per il Teorema 2.7, la successione (aβn + bαn + αn βn ) è infinitesimale. L'affermazione 2) segue dalla rappresentazione (2.5) del Lemma 2.1.
Passiamo all'affermazione 3). Per condizione, lim yn = b 6= 0. In virtù del Teorema 2.3. la successione (|yn |) converge e lim |yn | = |b| 6= 0. Pertanto, dato il numero ε = |b|/2, esiste un numero N tale che n > N
0 < | 2 b| = |b| −
Pertanto, yn =6 0 e 3|b|< y n < |b| , n >N.
Pertanto, il quoziente xn /yn è definito per ogni n > N, e la sequenza (1/yn) è limitata. Consideriamo per tutti gli n > N la differenza
(αn b − aβn ). |
|||||||||||||||||||||
Sotto sequenza |
αn b |
aβn |
Infinitamente piccolo |
||||||||||||||||||
limitato. Per il Teorema 2.8 la successione |
|||||||||||||||||||||
− b |
|||||||||||||||||||||
molto piccolo. Pertanto, per il Lemma 2.1, l'affermazione 3) è dimostrata. Corollario 1. Se la successione (xn) converge, allora per qualsiasi
Per ogni numero c, la successione (c · xn ) converge e lim(cxn ) = c · lim xn .
Funzioni infinitesime
Viene richiamata la funzione %%f(x)%%. infinitesimale(b.m.) con %%x \to a \in \overline(\mathbb(R))%%, se con questa tendenza dell'argomento il limite della funzione è pari a zero.
Il concetto di b.m. la funzione è indissolubilmente legata alle istruzioni per cambiare il suo argomento. Possiamo parlare di b.m. funziona in %%a \to a + 0%% e in %%a \to a - 0%%. Di solito b.m. le funzioni sono indicate dalle prime lettere dell'alfabeto greco %%\alpha, \beta, \gamma, \ldots%%
Esempi
- La funzione %%f(x) = x%% è b.m. a %%x \to 0%%, poiché il suo limite nel punto %%a = 0%% è zero. Secondo il teorema sulla connessione tra limite bilaterale e limite unilaterale, questa funzione è b.m. sia con %%x \to +0%% che con %%x \to -0%%.
- Funzione %%f(x) = 1/(x^2)%% - b.m. in %%x \to \infty%% (così come in %%x \to +\infty%% e in %%x \to -\infty%%).
Un numero costante diverso da zero, non importa quanto piccolo in valore assoluto, non è un b.m. funzione. Per i numeri costanti, l'unica eccezione è zero, poiché la funzione %%f(x) \equiv 0%% ha un limite pari a zero.
Teorema
La funzione %%f(x)%% ha nel punto %%a \in \overline(\mathbb(R))%% della linea numerica estesa un limite finale pari al numero %%b%% se e solo se questa funzione è uguale alla somma di questo numero %%b%% e b.m. funzioni %%\alpha(x)%% con %%x \to a%%, oppure $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Leftrightarrow \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\right). $$
Proprietà delle funzioni infinitesime
Secondo le regole del passaggio al limite con %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, seguono le seguenti affermazioni:
- La somma del numero finale di b.m. funzioni per %%x \to a%% è b.m. al %%x \al a%%.
- Il prodotto di qualsiasi numero b.m. funzioni per %%x \to a%% è b.m. al %%x \al a%%.
Prodotto b.m. funzioni in %%x \to a%% e una funzione limitata in un quartiere perforato %%\stackrel(\circ)(\text(U))(a)%% del punto a, c'è b.m. alla funzione %%x \to a%%.
È chiaro che il prodotto di una funzione costante e b.m. in %%x \to a%% c'è b.m. funzione a %%x \to a%%.
Funzioni infinitesime equivalenti
Vengono chiamate le funzioni infinitesime %%\alpha(x), \beta(x)%% per %%x \to a%% equivalente e scrivi %%\alpha(x) \sim \beta(x)%%, if
$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alpha(x))) = 1. $$
Teorema sulla sostituzione di b.m. funzioni equivalenti
Sia %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% essere b.m. funzioni per %%x \to a%%, con %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, quindi $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ limiti_(x \to a)(\frac(\alpha_1(x))(\beta_1(x))). $$
B.m. equivalente funzioni.
Sia %%\alpha(x)%% b.m. funzione in %%x \to a%%, quindi
- %%\sin(\alpha(x)) \sim \alpha(x)%%
- %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
- %%\tan \alpha(x) \sim \alpha(x)%%
- %%\arcsin\alpha(x) \sim \alpha(x)%%
- %%\arctan\alpha(x) \sim \alpha(x)%%
- %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
- %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
- %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%
Esempio
$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(array) $$
Funzioni infinitamente grandi
Viene richiamata la funzione %%f(x)%%. infinitamente grande(b.b.) con %%x \to a \in \overline(\mathbb(R))%%, se con questa tendenza dell'argomento la funzione ha limite infinito.
Simile a b.m. concetto di funzioni b.b. la funzione è indissolubilmente legata alle istruzioni per cambiare il suo argomento. Possiamo parlare di b.b. funziona con %%x \to a + 0%% e %%x \to a - 0%%. Il termine “infinitamente grande” non parla del valore assoluto della funzione, ma della natura del suo cambiamento in prossimità del punto in questione. Nessun numero costante, per quanto grande in valore assoluto, è infinitamente grande.
Esempi
- Funzione %%f(x) = 1/x%% - b.b. al %%x \allo 0%%.
- Funzione %%f(x) = x%% - b.b. al %%x \to \infty%%.
Se le condizioni di definizione $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(array) $$
poi ne parlano positivo O negativo b.b. alla funzione %%a%%.
Esempio
Funzione %%1/(x^2)%% - positivo b.b. al %%x \allo 0%%.
Il collegamento tra b.b. e b.m. funzioni
Se %%f(x)%% è b.b. con la funzione %%x \to a%%, quindi %%1/f(x)%% - b.m.
al %%x \al a%%. Se %%\alpha(x)%% - b.m. poiché %%x \to a%% è una funzione diversa da zero in qualche zona perforata del punto %%a%%, allora %%1/\alpha(x)%% è b.b. al %%x \al a%%.
Proprietà delle funzioni infinitamente grandi
Presentiamo diverse proprietà del b.b. funzioni. Queste proprietà derivano direttamente dalla definizione di b.b. funzioni e proprietà delle funzioni aventi limiti finiti, nonché dal teorema sulla connessione tra b.b. e b.m. funzioni.
- Il prodotto di un numero finito di b.b. funzioni per %%x \to a%% è b.b. funzione a %%x \to a%%. Infatti, se %%f_k(x), k = \overline(1, n)%% - b.b. funziona in %%x \to a%%, quindi in qualche zona perforata del punto %%a%% %%f_k(x) \ne 0%%, e dal teorema di connessione b.b. e b.m. funzioni %%1/f_k(x)%% - b.m. funzione a %%x \to a%%. Risulta %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - funzione b.m per %%x \to a%% e %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funzione a %%x \to a%%.
- Prodotto b.b. funzioni per %%x \to a%% e una funzione che in qualche zona perforata del punto %%a%% in valore assoluto è maggiore di una costante positiva è b.b. funzione a %%x \to a%%. In particolare il prodotto b.b. una funzione con %%x \to a%% e una funzione che ha un limite finito diverso da zero nel punto %%a%% sarà b.b. funzione a %%x \to a%%.
La somma di due b.b. funzioni in %%x \to a%% c'è incertezza. A seconda del segno dei termini, la natura della variazione di tale somma può essere molto diversa.
Esempio
Siano date le funzioni %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. funzioni in %%x \to \infty%%. Poi:
- %%f(x) + g(x) = 3x%% - b.b. funzione a %%x \to \infty%%;
- %%f(x) + h(x) = 0%% - b.m. funzione a %%x \to \infty%%;
- %%h(x) + v(x) = \sin x%% non ha limiti a %%x \to \infty%%.
La somma di una funzione limitata in un intorno forato del punto %%a%% e b.b. le funzioni con %%x \to a%% sono b.b. funzione a %%x \to a%%.
Ad esempio, le funzioni %%x - \sin x%% e %%x + \cos x%% sono b.b. al %%x \to \infty%%.
