უსასრულოდ მცირე მიმდევრობა - განმარტება და თვისებები. მაგალითები რა რაოდენობას ეწოდება უსასრულო მცირე
უსასრულო და დიდის გამოთვლა
უსასრულოდ მცირე გაანგარიშება- უსასრულო სიდიდეებით შესრულებული გამოთვლები, რომლებშიც მიღებული შედეგი განიხილება როგორც უსასრულო მცირეთა უსასრულო ჯამი. უსასრულო მცირეთა გამოთვლა არის დიფერენციალური და ინტეგრალური გამოთვლების ზოგადი კონცეფცია, რომელიც საფუძვლად უდევს თანამედროვე უმაღლესი მათემატიკას. უსასრულო სიდიდის ცნება მჭიდროდაა დაკავშირებული ლიმიტის ცნებასთან.
უსასრულოდ მცირე
ქვემიმდევრობა ა ნდაურეკა უსასრულოდ მცირე, თუ . მაგალითად, რიცხვების თანმიმდევრობა უსასრულოდ მცირეა.
ფუნქციას ეძახიან უსასრულო პატარა წერტილის სიახლოვეს x 0 თუ ![]() .
.
ფუნქციას ეძახიან უსასრულოდ მცირე უსასრულობაში, თუ ![]() ან
ან ![]() .
.
ასევე უსასრულოდ მცირე არის ფუნქცია, რომელიც არის განსხვავება ფუნქციასა და მის ზღვარს შორის, ანუ თუ ![]() , ეს ვ(x) − ა = α( x)
, .
, ეს ვ(x) − ა = α( x)
, .
უსაზღვროდ დიდი რაოდენობით
ყველა ქვემოთ მოცემულ ფორმულაში, უსასრულობა თანასწორობის მარჯვნივ იგულისხმება გარკვეული ნიშნით (ან „პლუს“ ან „მინუს“). ეს არის, მაგალითად, ფუნქცია xცოდვა x, შეუზღუდავი ორივე მხრიდან, არ არის უსასრულოდ დიდი ზე.
ქვემიმდევრობა ა ნდაურეკა უსასრულოდ დიდი, თუ ![]() .
.
ფუნქციას ეძახიან უსასრულოდ დიდი წერტილის სიახლოვეს x 0 თუ ![]() .
.
ფუნქციას ეძახიან უსასრულოდ დიდი უსასრულობაში, თუ ![]() ან
ან ![]() .
.
უსასრულოდ მცირე და უსასრულოდ დიდის თვისებები
უსასრულოდ მცირე სიდიდეების შედარება
როგორ შევადაროთ უსასრულოდ მცირე რაოდენობა?
უსასრულო სიდიდეების თანაფარდობა ქმნის ე.წ.
განმარტებები
დავუშვათ, რომ გვაქვს უსასრულო მცირე მნიშვნელობები α( x) და β( x) (ან, რაც არ არის მნიშვნელოვანი განმარტებისთვის, უსასრულოდ მცირე მიმდევრობები).
ასეთი ლიმიტების გამოსათვლელად მოსახერხებელია L'Hopital-ის წესის გამოყენება.
შედარების მაგალითები
გამოყენება შესახებ-სიმბოლიკა, მიღებული შედეგები შეიძლება ჩაიწეროს შემდეგი ფორმით x 5 = ო(x 3). ამ შემთხვევაში, შემდეგი ჩანაწერები მართალია: 2x 2 + 6x = ო(x) და x = ო(2x 2 + 6x).ექვივალენტური მნიშვნელობები
განმარტება
თუ , მაშინ α და β უსასრულო სიდიდეებს უწოდებენ ექვივალენტი ().
აშკარაა, რომ ეკვივალენტური სიდიდეები არის ერთი და იგივე სიმცირის რიგის უსასრულო სიდიდის განსაკუთრებული შემთხვევა.
როდესაც შემდეგი ეკვივალენტური მიმართებები მოქმედებს (როგორც ე.წ. აღსანიშნავი ლიმიტების შედეგები):
თეორემა
ორი უსასრულო სიდიდის კოეფიციენტის (ფარდობის) ზღვარი არ შეიცვლება, თუ ერთი მათგანი (ან ორივე) შეიცვლება ეკვივალენტური რაოდენობით..ამ თეორემას აქვს პრაქტიკული მნიშვნელობა ლიმიტების პოვნისას (იხ. მაგალითი).
გამოყენების მაგალითი
ჩანაცვლება სმენ 2x ექვივალენტური ღირებულება 2 x, ვიღებთისტორიული ჩანახატი
"უსასრულოდ მცირე" კონცეფცია განიხილებოდა ჯერ კიდევ ძველ დროში განუყოფელი ატომების კონცეფციასთან დაკავშირებით, მაგრამ არ იყო შეტანილი კლასიკურ მათემატიკაში. იგი კვლავ აღორძინდა მე-16 საუკუნეში „განყოფის მეთოდის“ მოსვლასთან ერთად - შესასწავლი ფიგურის დაყოფა უსასრულოდ მცირე მონაკვეთებად.
მე-17 საუკუნეში მოხდა უსასრულოდ მცირე გამოთვლების ალგებრიზაცია. მათი განსაზღვრა დაიწყეს, როგორც რიცხვითი სიდიდეები, რომლებიც ნაკლებია ნებისმიერ სასრულ (არანულოვან) სიდიდეზე და მაინც არ არის ნულის ტოლი. ანალიზის ხელოვნება მდგომარეობდა უსასრულო მცირე ზომის (დიფერენციალების) შემცველი მიმართების შედგენაში და შემდეგ მის ინტეგრირებაში.
ძველი სკოლის მათემატიკოსებმა ეს კონცეფცია გამოსცადეს უსასრულოდ მცირემკაცრი კრიტიკა. მიშელ როლელმა დაწერა, რომ ახალი გაანგარიშება არის " გენიალური შეცდომების ნაკრები"; ვოლტერმა კაუსტიკურად შენიშნა, რომ კალკულუსი არის ნივთების გამოთვლისა და ზუსტად გაზომვის ხელოვნება, რომელთა არსებობის დამტკიცება შეუძლებელია. ჰაიგენსმაც კი აღიარა, რომ მას არ ესმოდა უმაღლესი წოდების დიფერენციალური მნიშვნელობა.
ბედის ირონიად შეიძლება ჩაითვალოს არასტანდარტული ანალიზის საუკუნის შუა ხანებში გაჩენა, რამაც დაამტკიცა, რომ თავდაპირველი თვალსაზრისი - ფაქტობრივი უსასრულო - ასევე თანმიმდევრული იყო და შეიძლება გამოეყენებინათ ანალიზისთვის.
იხილეთ ასევე
ფონდი ვიკიმედია. 2010 წელი.
ნახეთ, რა არის „უსასრულოდ მცირე რაოდენობა“ სხვა ლექსიკონებში:
უსაზღვროდ მცირე რაოდენობით- ცვლადი სიდიდე გარკვეულ პროცესში, თუ ამ პროცესში ის უსასრულოდ უახლოვდება (მიდრეკილია) ნულამდე... დიდი პოლიტექნიკური ენციკლოპედია
უსასრულოდ მცირე- ■ რაღაც უცნობი, მაგრამ დაკავშირებული ჰომეოპათიასთან... საერთო ჭეშმარიტების ლექსიკა
უსასრულო პატარა ფუნქციები და მათი ძირითადი თვისებები
ფუნქცია y=f(x)დაურეკა უსასრულოდ მცირეზე x→aან როდის x→∞, თუ ან , ე.ი. უსასრულოდ მცირე ფუნქცია არის ფუნქცია, რომლის ზღვარი მოცემულ წერტილში არის ნული.
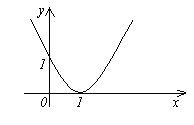
მაგალითები.
მოდით დავამყაროთ შემდეგი მნიშვნელოვანი ურთიერთობა:
თეორემა.თუ ფუნქცია y=f(x)წარმომადგენლობით x→aროგორც მუდმივი რიცხვის ჯამი ბდა უსასრულოდ მცირე სიდიდე α(x): f (x)=b+ α(x)რომ .
პირიქით, თუ, მაშინ f (x)=b+α(x), სად ნაჯახი)– უსასრულოდ მცირე ზე x→a.
მტკიცებულება.
განვიხილოთ უსასრულოდ მცირე ფუნქციების ძირითადი თვისებები.
თეორემა 1.ორი, სამი და ზოგადად ნებისმიერი სასრული რაოდენობის უსასრულო რიცხვის ალგებრული ჯამი უსასრულო მცირე ფუნქციაა.
მტკიცებულება. მოდით დავამტკიცოთ ორი ტერმინი. დაე f(x)=α(x)+β(x), სად და . ჩვენ უნდა დავამტკიცოთ, რომ ნებისმიერი თვითნებური მცირე ε > ნაპოვნია 0 δ> 0, ისეთი, რომ ამისთვის x, უთანასწორობის დაკმაყოფილება |x – a|<δ , შესრულებული |f(x)|< ε.
მაშ ასე, დავაფიქსიროთ თვითნებური რიცხვი ε > 0. ვინაიდან თეორემის პირობების მიხედვით α(x)არის უსასრულოდ მცირე ფუნქცია, მაშინ არის ასეთი δ 1 > 0, რაც არის |x – a|< δ 1 გვაქვს |α(x)|< ε / 2. ანალოგიურად, მას შემდეგ β(x)არის უსასრულოდ მცირე, მაშინ არის ასეთი δ 2 > 0, რაც არის |x – a|< δ 2 გვაქვს | β(x)|< ε / 2.
Მოდი ავიღოთ δ=წთ(δ 1 , δ2 } .მერე პუნქტის მეზობლად არადიუსი δ თითოეული უტოლობა დაკმაყოფილდება |α(x)|< ε / 2 და | β(x)|< ε / 2. ამიტომ, ამ სამეზობლოში იქნება
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
იმათ. |f(x)|< ε, რაც დასამტკიცებელია.
თეორემა 2.უსასრულოდ მცირე ფუნქციის პროდუქტი ნაჯახი)შეზღუდული ფუნქციისთვის f(x)ზე x→a(ან როდის x→∞) არის უსასრულო მცირე ფუნქცია.
მტკიცებულება. ფუნქციიდან გამომდინარე f(x)შეზღუდულია, მაშინ არის რაოდენობა მისეთი, რომ ყველა ღირებულებისთვის xპუნქტის რომელიღაც უბნიდან a|f(x)|≤M.უფრო მეტიც, მას შემდეგ ნაჯახი)არის უსასრულოდ მცირე ფუნქცია x→a, შემდეგ თვითნებური ε > 0 არის წერტილის სამეზობლო ა, რომელშიც უთანასწორობა შენარჩუნდება |α(x)|< ε /მ. შემდეგ ამ უბნებიდან უფრო პატარა გვაქვს | αf|< ε /მ= ე. და ეს იმას ნიშნავს აფ- უსასრულოდ მცირე. შემთხვევისთვის x→∞მტკიცებულება ხორციელდება ანალოგიურად.
დადასტურებული თეორემიდან გამომდინარეობს:
დასკვნა 1.თუ და, მაშინ.
დასკვნა 2.თუ c=კონსტ, მაშინ.
თეორემა 3.უსასრულოდ მცირე ფუნქციის თანაფარდობა α(x)თითო ფუნქციაზე f(x), რომლის ზღვარი განსხვავდება ნულისაგან, უსასრულოდ მცირე ფუნქციაა.
მტკიცებულება. დაე ![]() . შემდეგ 1 /f(x)არის შეზღუდული ფუნქცია. ამიტომ წილადი
. შემდეგ 1 /f(x)არის შეზღუდული ფუნქცია. ამიტომ წილადი ![]() არის უსასრულოდ მცირე ფუნქციისა და შეზღუდული ფუნქციის ნამრავლი, ე.ი. ფუნქცია უსასრულოდ მცირეა.
არის უსასრულოდ მცირე ფუნქციისა და შეზღუდული ფუნქციის ნამრავლი, ე.ი. ფუნქცია უსასრულოდ მცირეა.
უსასრულოდ მცირე და უსასრულოდ დიდ ფუნქციებს შორის ურთიერთობა
თეორემა 1.თუ ფუნქცია f(x)არის უსასრულოდ დიდი at x→a, შემდეგ ფუნქცია 1 /f(x)არის უსასრულოდ მცირე x→a.
მტკიცებულება.ავიღოთ თვითნებური რიცხვი ε >0 და აჩვენე ეს ზოგიერთს δ>0 (დამოკიდებულია ε) ყველასთვის x, რისთვისაც |x – a|<δ , უთანასწორობა დაკმაყოფილებულია და ეს იმას ნიშნავს 1/f(x)უსასრულოდ მცირე ფუნქციაა. მართლაც, მას შემდეგ f(x)არის უსასრულოდ დიდი ფუნქცია at x→a, მაშინ იქნება δ>0 ისეთი რომ როგორც კი |x – a|<δ , ასე | f(x)|> 1/ ე. მაგრამ შემდეგ იგივე x.
მაგალითები.
საპირისპირო თეორემაც შეიძლება დადასტურდეს.
თეორემა 2.თუ ფუნქცია f(x)- უსასრულოდ მცირე ზე x→a(ან x→∞)და არ ქრება, მაშინ y= 1/f(x)უსასრულოდ დიდი ფუნქციაა.
თავად ჩაატარეთ თეორემის დადასტურება.
მაგალითები.
ამრიგად, უსასრულოდ მცირე და უსასრულოდ დიდი ფუნქციების უმარტივესი თვისებები შეიძლება ჩაიწეროს შემდეგი პირობითი ურთიერთობების გამოყენებით: ა≠ 0
ლიმიტის თეორემები
თეორემა 1.ორი, სამი და საერთოდ გარკვეული რაოდენობის ფუნქციების ალგებრული ჯამის ზღვარი უდრის ამ ფუნქციების ზღვრების ალგებრულ ჯამს, ე.ი.
მტკიცებულება. მოდით განვახორციელოთ მტკიცებულება ორი ტერმინისთვის, რადგან ეს შეიძლება გაკეთდეს იმავე გზით ნებისმიერი რაოდენობის ტერმინისთვის. დაე ![]() .მაშინ f(x)=b+α(x)და g(x)=c+β(x), სად α
და β
- უსასრულოდ მცირე ფუნქციები. აქედან გამომდინარე,
.მაშინ f(x)=b+α(x)და g(x)=c+β(x), სად α
და β
- უსასრულოდ მცირე ფუნქციები. აქედან გამომდინარე,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
იმიტომ რომ ბ+გარის მუდმივი და α(x) + β(x)არის უსასრულოდ მცირე ფუნქცია, მაშინ
მაგალითი. .
თეორემა 2.ორი, სამი და ზოგადად სასრული რაოდენობის ფუნქციების ნამრავლის ზღვარი ტოლია ამ ფუნქციების ზღვრების ნამრავლის:
მტკიცებულება. დაე ![]() . აქედან გამომდინარე, f(x)=b+α(x)და g(x)=c+β(x)და
. აქედან გამომდინარე, f(x)=b+α(x)და g(x)=c+β(x)და
fg = (b + α) (c + β) = bc + (bβ + cα + αβ).
მუშაობა ძვ.წარის მუდმივი მნიშვნელობა. ფუნქცია bβ + c α + αβუსასრულოდ მცირე ფუნქციების თვისებებზე დაყრდნობით, არსებობს უსასრულო სიდიდე. Ამიტომაც .
დასკვნა 1.მუდმივი ფაქტორი შეიძლება იქნას მიღებული ზღვრული ნიშნის მიღმა:
![]() .
.
დასკვნა 2.ხარისხის ლიმიტი უდრის ლიმიტის ხარისხს:
![]() .
.
მაგალითი.![]() .
.
თეორემა 3.ორი ფუნქციის კოეფიციენტის ზღვარი ტოლია ამ ფუნქციების ზღვრების კოეფიციენტის, თუ მნიშვნელის ზღვარი განსხვავდება ნულისაგან, ე.ი.
 .
.
მტკიცებულება. დაე . აქედან გამომდინარე, f(x)=b+α(x)და g(x)=c+β(x), სად α, β - უსასრულოდ მცირე. განვიხილოთ კოეფიციენტი
წილადი უსასრულოდ მცირე ფუნქციაა, რადგან მრიცხველი უსასრულო მცირე ფუნქციაა, ხოლო მნიშვნელს აქვს ზღვარი. c 2 ≠0.
მაგალითები.

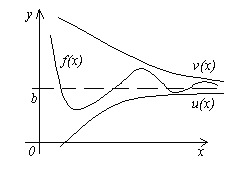
თეორემა 4.მიეცით სამი ფუნქცია f(x), u(x)და v(x), უტოლობების დაკმაყოფილება u (x)≤f(x)≤ v(x). თუ ფუნქციები u(x)და v(x)აქვს იგივე ლიმიტი x→a(ან x→∞), შემდეგ ფუნქცია f(x)მიდრეკილია იმავე ზღვარზე, ე.ი. თუ
![]() , რომ .
, რომ .
ამ თეორემის მნიშვნელობა ნათელია ფიგურიდან.
თეორემა 4-ის დადასტურება შეგიძლიათ ნახოთ, მაგალითად, სახელმძღვანელოში: Piskunov N. S. Differential and Integral Calculus, ტ. 1 - M.: Nauka, 1985 წ.
თეორემა 5.თუ ზე x→a(ან x→∞) ფუნქცია y=f(x)იღებს არაუარყოფით მნიშვნელობებს y≥0და ამავე დროს მიდრეკილია ზღვრამდე ბ, მაშინ ეს ზღვარი არ შეიძლება იყოს უარყოფითი: b≥0.
მტკიცებულება. ჩვენ მტკიცებულებას განვახორციელებთ წინააღმდეგობით. მოდი ვიჩვენოთ, რომ ბ<0 , მაშინ |y – b|≥|b|და, შესაბამისად, განსხვავების მოდული არ არის ნულისკენ მიდრეკილი, როდესაც x→a. Მაგრამ შემდეგ წარ აღწევს ზღვარს ბზე x→a, რაც ეწინააღმდეგება თეორემის პირობებს.
თეორემა 6.თუ ორი ფუნქცია f(x)და g(x)არგუმენტის ყველა მნიშვნელობისთვის xდააკმაყოფილეთ უთანასწორობა f(x)≥ g(x)და აქვს საზღვრები, მაშინ უთანასწორობა მოქმედებს b≥c.
მტკიცებულება.თეორემის პირობების მიხედვით f(x)-g(x) ≥0მაშასადამე, თეორემა 5-ით ![]() , ან
, ან ![]() .
.
ცალმხრივი ლიმიტები

აქამდე განვიხილეთ ფუნქციის ლიმიტის განსაზღვრა, როდესაც x→aთვითნებურად, ე.ი. ფუნქციის ლიმიტი არ იყო დამოკიდებული იმაზე, თუ როგორ მდებარეობდა იგი xმიმართ ა, მარცხნივ ან მარჯვნივ ა. თუმცა, საკმაოდ ხშირია ფუნქციების პოვნა, რომლებსაც არ აქვთ ლიმიტი ამ პირობით, მაგრამ მათ აქვთ ლიმიტი თუ x→a, რჩება ერთ მხარეს ამარცხნივ ან მარჯვნივ (იხ. სურათი). აქედან გამომდინარე, შემოღებულია ცალმხრივი ლიმიტების ცნებები.
თუ f(x)მიდრეკილია ზღვრამდე ბზე xთენდება გარკვეული რიცხვისკენ აᲘსე xიღებს მხოლოდ მნიშვნელობებს ნაკლები ა, მერე წერენ და ურეკავენ f(x) ფუნქციის ბლიმიტი a წერტილში მარცხნივ.
უსასრულო და დიდის გამოთვლა
უსასრულოდ მცირე გაანგარიშება- უსასრულო სიდიდეებით შესრულებული გამოთვლები, რომლებშიც მიღებული შედეგი განიხილება როგორც უსასრულო მცირეთა უსასრულო ჯამი. უსასრულო მცირეთა გამოთვლა არის დიფერენციალური და ინტეგრალური გამოთვლების ზოგადი კონცეფცია, რომელიც საფუძვლად უდევს თანამედროვე უმაღლესი მათემატიკას. უსასრულო სიდიდის ცნება მჭიდროდაა დაკავშირებული ლიმიტის ცნებასთან.
უსასრულოდ მცირე
ქვემიმდევრობა ა ნდაურეკა უსასრულოდ მცირე, თუ . მაგალითად, რიცხვების თანმიმდევრობა უსასრულოდ მცირეა.
ფუნქციას ეძახიან უსასრულო პატარა წერტილის სიახლოვეს x 0 თუ ![]() .
.
ფუნქციას ეძახიან უსასრულოდ მცირე უსასრულობაში, თუ ![]() ან
ან ![]() .
.
ასევე უსასრულოდ მცირე არის ფუნქცია, რომელიც არის განსხვავება ფუნქციასა და მის ზღვარს შორის, ანუ თუ ![]() , ეს ვ(x) − ა = α( x)
, .
, ეს ვ(x) − ა = α( x)
, .
უსაზღვროდ დიდი რაოდენობით
ქვემიმდევრობა ა ნდაურეკა უსასრულოდ დიდი, თუ ![]() .
.
ფუნქციას ეძახიან უსასრულოდ დიდი წერტილის სიახლოვეს x 0 თუ ![]() .
.
ფუნქციას ეძახიან უსასრულოდ დიდი უსასრულობაში, თუ ![]() ან
ან ![]() .
.
ყველა შემთხვევაში, უსასრულობა თანასწორობის უფლებით იგულისხმება გარკვეული ნიშნით (ან „პლუს“ ან „მინუს“). ეს არის, მაგალითად, ფუნქცია xცოდვა xარ არის უსასრულოდ დიდი at.
უსასრულოდ მცირე და უსასრულოდ დიდის თვისებები
უსასრულოდ მცირე სიდიდეების შედარება
როგორ შევადაროთ უსასრულოდ მცირე რაოდენობა?
უსასრულო სიდიდეების თანაფარდობა ქმნის ე.წ.
განმარტებები
დავუშვათ, რომ გვაქვს უსასრულო მცირე მნიშვნელობები α( x) და β( x) (ან, რაც არ არის მნიშვნელოვანი განმარტებისთვის, უსასრულოდ მცირე მიმდევრობები).
ასეთი ლიმიტების გამოსათვლელად მოსახერხებელია L'Hopital-ის წესის გამოყენება.
შედარების მაგალითები
გამოყენება შესახებ-სიმბოლიკა, მიღებული შედეგები შეიძლება ჩაიწეროს შემდეგი ფორმით x 5 = ო(x 3). ამ შემთხვევაში, შემდეგი ჩანაწერები მართალია: 2x 2 + 6x = ო(x) და x = ო(2x 2 + 6x).ექვივალენტური მნიშვნელობები
განმარტება
თუ , მაშინ α და β უსასრულო სიდიდეებს უწოდებენ ექვივალენტი ().
აშკარაა, რომ ეკვივალენტური სიდიდეები არის ერთი და იგივე სიმცირის რიგის უსასრულო სიდიდის განსაკუთრებული შემთხვევა.
როდესაც შემდეგი ეკვივალენტური მიმართებები მოქმედებს: , , ![]() .
.
თეორემა
ორი უსასრულო სიდიდის კოეფიციენტის (ფარდობის) ზღვარი არ შეიცვლება, თუ ერთი მათგანი (ან ორივე) შეიცვლება ეკვივალენტური რაოდენობით..ამ თეორემას აქვს პრაქტიკული მნიშვნელობა ლიმიტების პოვნისას (იხ. მაგალითი).
გამოყენების მაგალითი
ჩანაცვლება სმენ 2x ექვივალენტური ღირებულება 2 x, ვიღებთისტორიული ჩანახატი
"უსასრულოდ მცირე" კონცეფცია განიხილებოდა ჯერ კიდევ ძველ დროში განუყოფელი ატომების კონცეფციასთან დაკავშირებით, მაგრამ არ იყო შეტანილი კლასიკურ მათემატიკაში. იგი კვლავ აღორძინდა მე-16 საუკუნეში „განყოფის მეთოდის“ მოსვლასთან ერთად - შესასწავლი ფიგურის დაყოფა უსასრულოდ მცირე მონაკვეთებად.
მე-17 საუკუნეში მოხდა უსასრულოდ მცირე გამოთვლების ალგებრიზაცია. მათი განსაზღვრა დაიწყეს, როგორც რიცხვითი სიდიდეები, რომლებიც ნაკლებია ნებისმიერ სასრულ (არანულოვან) სიდიდეზე და მაინც არ არის ნულის ტოლი. ანალიზის ხელოვნება მდგომარეობდა უსასრულო მცირე ზომის (დიფერენციალების) შემცველი მიმართების შედგენაში და შემდეგ მის ინტეგრირებაში.
ძველი სკოლის მათემატიკოსებმა ეს კონცეფცია გამოსცადეს უსასრულოდ მცირემკაცრი კრიტიკა. მიშელ როლელმა დაწერა, რომ ახალი გაანგარიშება არის " გენიალური შეცდომების ნაკრები"; ვოლტერმა კაუსტიკურად შენიშნა, რომ კალკულუსი არის ნივთების გამოთვლისა და ზუსტად გაზომვის ხელოვნება, რომელთა არსებობის დამტკიცება შეუძლებელია. ჰაიგენსმაც კი აღიარა, რომ მას არ ესმოდა უმაღლესი წოდების დიფერენციალური მნიშვნელობა.
პარიზის მეცნიერებათა აკადემიაში დავები ანალიზის დასაბუთებასთან დაკავშირებით იმდენად სკანდალური გახდა, რომ აკადემიამ ერთხელ სრულიად აუკრძალა თავის წევრებს ამ თემაზე საუბარი (ეს ძირითადად როლს და ვარინიონს ეხებოდა). 1706 წელს როლელმა საჯაროდ მოხსნა თავისი წინააღმდეგობები, მაგრამ დისკუსიები გაგრძელდა.
1734 წელს ცნობილმა ინგლისელმა ფილოსოფოსმა ეპისკოპოსმა ჯორჯ ბერკლიმ გამოაქვეყნა სენსაციური ბროშურა, რომელიც ცნობილია შემოკლებული სახელწოდებით. ანალიტიკოსი" მისი სრული სახელი: " ანალიტიკოსი ან დისკურსი, რომელიც მიმართულია ურწმუნო მათემატიკოსს, სადაც იკითხება, არის თუ არა თანამედროვე ანალიზის საგანი, პრინციპები და დასკვნები უფრო მკაფიოდ აღქმული ან უფრო მკაფიოდ, ვიდრე რელიგიური საიდუმლოებები და რწმენის სტატიები.».
ანალიტიკოსი შეიცავდა მახვილგონივრულ და მეტწილად სამართლიან კრიტიკას უსასრულოდ მცირე გაანგარიშების მიმართ. ბერკლიმ ჩათვალა ანალიზის მეთოდი ლოგიკას შეუსაბამოდ და დაწერა, რომ ” რაც არ უნდა სასარგებლო იყოს, ის მხოლოდ ერთგვარ გამოცნობად შეიძლება ჩაითვალოს; ოსტატური უნარი, ხელოვნება, უფრო სწორად, ხრიკი, მაგრამ არა როგორც მეცნიერული მტკიცებულების მეთოდი" ბერკლის ირონიულად ციტირებს ნიუტონის ფრაზას მიმდინარე რაოდენობების გაზრდის შესახებ „მათი წარმოშობის ან გაქრობის დასაწყისშივე“ ისინი არც სასრული რაოდენობებია, არც უსასრულოდ მცირე და არც არაფერი. არ შეიძლება მათ გარდაცვლილი სიდიდის აჩრდილები ვუწოდოთ?... და საერთოდ როგორ შეიძლება ვისაუბროთ იმ საგნებს შორის ურთიერთობაზე, რომლებსაც სიდიდე არ გააჩნიათ? განსხვავება, არ უნდა, რადგან მეჩვენება, რომ თეოლოგიაში რაღაცის ბრალია».
შეუძლებელია, წერს ბერკლი, წარმოვიდგინოთ მყისიერი სიჩქარე, ანუ სიჩქარე მოცემულ მომენტში და მოცემულ წერტილში, რადგან მოძრაობის ცნება მოიცავს (სასრული არანულოვანი) სივრცისა და დროის ცნებებს.
როგორ იძლევა ანალიზი სწორ შედეგებს? ბერკლი მივიდა იმ აზრამდე, რომ ეს აიხსნება ანალიტიკურ დასკვნებში რამდენიმე შეცდომის არსებობით და ეს პარაბოლის მაგალითით აჩვენა. საინტერესოა, რომ ზოგიერთი ძირითადი მათემატიკოსი (მაგალითად, ლაგრანჟი) დაეთანხმა მას.
პარადოქსული სიტუაცია შეიქმნა, როდესაც მათემატიკაში სიმკაცრე და ნაყოფიერება ერთმანეთს ერეოდა. არასწორად განსაზღვრული ცნებებით უკანონო ქმედებების გამოყენების მიუხედავად, პირდაპირი შეცდომების რაოდენობა საოცრად მცირე იყო - ინტუიცია მოვიდა სამაშველოში. და მაინც, მთელი მე-18 საუკუნის განმავლობაში, მათემატიკური ანალიზი სწრაფად ვითარდებოდა, არსებითად ყოველგვარი დასაბუთების გარეშე. მისი ეფექტურობა გასაოცარი იყო და თავისთავად ლაპარაკობდა, მაგრამ დიფერენციალის მნიშვნელობა ჯერ კიდევ გაურკვეველი იყო. ფუნქციისა და მისი წრფივი ნაწილის უსასრულოდ მცირე ზრდა განსაკუთრებით ხშირად აირია.
მთელი მე-18 საუკუნის მანძილზე უზარმაზარი ძალისხმევა ხორციელდებოდა სიტუაციის გამოსასწორებლად და მათში მონაწილეობდნენ საუკუნის საუკეთესო მათემატიკოსები, მაგრამ მხოლოდ კოშიმ მოახერხა ანალიზის საფუძვლის დამაჯერებლად აგება XIX საუკუნის დასაწყისში. მან მკაცრად განსაზღვრა ძირითადი ცნებები - ლიმიტი, კონვერგენცია, უწყვეტობა, დიფერენციალი და ა.შ., რის შემდეგაც მეცნიერებიდან გაქრა ფაქტობრივი უსასრულობა. ზოგიერთი დარჩენილი დახვეწილობა მოგვიანებით იყო ახსნილი
თეორემა 2.4. თუ (x n) და (y n) თანმიმდევრობები ერთმანეთს ემთხვევა და x n ≤ y n, n > n 0, მაშინ lim x n ≤ lim y n.
მოდით lim xn = a, |
lim yn = b და a > b. განმარტებით 2.4 ლიმიტები |
||||||||||||||||||||
თანმიმდევრობები რიცხვით ε = |
არის N რიცხვი ისეთი, რომ |
||||||||||||||||||||
ამიტომ, n > max(n0, N) yn< |
< xn , что противоречит |
||||||||||||||||||||
მდგომარეობა. |
|||||||||||||||||||||
კომენტარი. თუ (xn), (yn) თანმიმდევრობები ერთმანეთს ემთხვევა |
|||||||||||||||||||||
ყველა n > n0 |
xn< yn , то можно утверждать лишь, что lim xn |
≤ lim yn . |
|||||||||||||||||||
ამის სანახავად საკმარისია მიმდევრობების გათვალისწინება
და yn = |
||||
შემდეგი შედეგები პირდაპირ გამომდინარეობს განმარტებიდან 2.4.
თეორემა 2.5. თუ რიცხვთა თანმიმდევრობა (x n) იყრის თავს და lim x n< b (b R), то N N: x n < b, n >ნ.
შედეგი. თუ მიმდევრობა (xn) იყრის თავს და lim xn 6= 0, მაშინ
N N: sgn xn = sgn(lim xn), n > N.
თეორემა 2.6. მოდით, მიმდევრობები (x n), (y n), (z n) აკმაყოფილებდეს პირობებს:
1) x n ≤ yn ≤ zn, n > n0,
2) თანმიმდევრობები(x n) და (z n) იყრიან თავს და lim x n = lim z n = a.
შემდეგ მიმდევრობა (y n ) იყრის თავს და lim y n = a.
2.1.3 უსასრულოდ მცირე თანმიმდევრობა
განმარტება 2.7. რიცხვთა თანმიმდევრობას (x n) ეწოდება უსასრულოდ მცირე (უსასრულოდ მცირე), თუ ის იყრის თავს და lim x n = 0.
რიცხვების მიმდევრობის ლიმიტის 2.4 განმარტების მიხედვით, განმარტება 2.7 უდრის შემდეგს:
განმარტება 2.8. რიცხვთა მიმდევრობას (x n) ეწოდება უსასრულო მცირე, თუ რომელიმე დადებითი რიცხვისთვის ε არის რიცხვი N = N(ε) ისეთი, რომ ყველა n > N-სთვის ამ მიმდევრობის x n ელემენტი აკმაყოფილებდეს უტოლობას |x n |< ε.
ასე რომ, (xn) - ბ.მ. ε > 0 N = N(ε) : n > N |xn |< ε.
მაგალითებიდან 2, 3 და შენიშვნა 1 თეორემა 2.3-მდე მივიღებთ, რომ შემდეგ
მოქმედების ( |
q−n |
არიან უსასრულო |
||||||||||||
უსასრულოდ მცირე მიმდევრობების თვისებები აღწერილია შემდეგი თეორემებით.
თეორემა 2.7. უსასრულო რაოდენობის უსასრულო მიმდევრობების ჯამი არის უსასრულო მცირე მიმდევრობა.
დაე, მიმდევრობები (xn), (yn) იყოს უსასრულოდ მცირე. ვაჩვენოთ, რომ (xn + yn) ასევე იქნება ერთი. დავაყენოთ ε > 0. მაშინ არის რიცხვი
N1 = N1 (ε) ისეთი, რომ |
||||
|xn |< |
N>N1, |
|||
და არის რიცხვი N2 = N2 (ε) ისეთი, რომ |
||||
|yn |< |
N>N2. |
|||
ავღნიშნოთ N = max(N1, N2). n > N-ისთვის, უტოლობები (2.1) და (2.2) იქნება მართებული. ამიტომ, n > N-სთვის
|xn + yn | ≤ |xn | + |ინ |< 2 + 2 = ε.
ეს ნიშნავს, რომ თანმიმდევრობა (xn +yn) არის უსასრულოდ მცირე. დებულება სასრული რაოდენობის უსასრულო მიმდევრობების ჯამის შესახებ
ეს გამომდინარეობს იქიდან, რაც დადასტურდა ინდუქციით.
თეორემა 2.8. უსასრულოდ მცირე მიმდევრობისა და შემოსაზღვრული მიმდევრობის ნამრავლი უსასრულოდ მცირეა.
მოდით (xn) იყოს შემოსაზღვრული და (yn) უსასრულოდ მცირე მიმდევრობა. შემოსაზღვრული მიმდევრობის 2.6 განმარტებით არის რიცხვი M > 0 ისეთი, რომ
|xn | ≤ M, n N. |
დავაფიქსიროთ თვითნებური რიცხვი ε > 0. ვინაიდან (yn) არის უსასრულო მცირე მიმდევრობა, არსებობს რიცხვი N = N(ε) ისეთი, რომ
ამიტომ თანმიმდევრობა (xn yn ) არის უსასრულოდ მცირე.

დასკვნა 1. უსასრულოდ მცირე მიმდევრობისა და კონვერგენტული მიმდევრობის ნამრავლი არის უსასრულოდ მცირე მიმდევრობა.
დასკვნა 2. ორი უსასრულო მიმდევრობის ნამრავლი არის უსასრულოდ მცირე მიმდევრობა.
უსასრულოდ მცირე მიმდევრობების გამოყენებით, კონვერგენტული მიმდევრობის განმარტება შეიძლება განსხვავებულად იქნას განხილული.
ლემა 2.1. იმისათვის, რომ რიცხვი იყოს რიცხვითი მიმდევრობის ზღვარი (x n), აუცილებელია და საკმარისია წარმოდგენა x n = a + α n, n N, რომელშიც (α n) არის უსასრულო მიმდევრობა.
აუცილებლობა. მოდით lim xn = a და a R. მაშინ
ε > 0 N = N(ε) N: n > N |xn − a|< ε.
თუ დავაყენებთ αn = xn − a, n N, მაშინ მივიღებთ, რომ (αn) არის უსასრულო მცირე მიმდევრობა და xn = a + αn, n N.
ადეკვატურობა. მოდით, მიმდევრობა (xn) იყოს ისეთი, რომ არსებობდეს რიცხვი a, რომლისთვისაც xn = a + αn, n N და lim αn = 0. დავაფიქსიროთ თვითნებური დადებითი რიცხვი ε. ვინაიდან lim αn = 0, მაშინ არის რიცხვი N = N(ε) N ისეთი, რომ |αn |< ε, n >N. ანუ სხვა აღნიშვნებში n > N |xn − a|< ε. Это означает, что lim xn = a.
მოდით გამოვიყენოთ ლემა 2.1 მნიშვნელოვან კონკრეტულ მაგალითზე.
ლემა 2.2. lim n n = 1.
√ √
ვინაიდან ყველასთვის n > 1 n n > 1, მაშინ n n = 1 + αn , და αn > 0 ამისთვის
ყველა n > 1. ამიტომ n = (1 + α |
)n = 1 + nα |
+ αn. |
|||||||||||||||
ვინაიდან ყველა ტერმინი დადებითია, ნ |
|||||||||||||||||
მოდით ε > 0. ვინაიდან |
2/ნ< ε для всех n >2/ε , მაშინ, ვარაუდით |
||||||||||||||||
N = max(1, ), მივიღებთ 0-ს< αn < ε, n >N. ამიტომ,
თანმიმდევრობა (αn) არის უსასრულოდ მცირე და, ლემის მიხედვით
2.1, lim n n = 1. √
შედეგი. თუ a > 1, მაშინ lim n a = 1.√ √
განცხადება გამომდინარეობს უტოლობებიდან 1< n a ≤ n n , n >[ა].
2.1.4 არითმეტიკული მოქმედებები მიმდევრობით
ლემა 2.1-ის და უსასრულოდ მცირე მიმდევრობების თვისებების გამოყენებით, ადვილია თეორემების მიღება კონვერგენტული მიმდევრობებიდან არითმეტიკული მოქმედებების გამოყენებით მიღებული მიმდევრობების ზღვრებზე.

|ბ| 3|ბ|
2 < |y n | < 2
თეორემა 2.9. მოდით, რიცხვების მიმდევრობა (x n) და (y n) გადავიდეს. შემდეგ მოქმედებს შემდეგი განცხადებები:
1) თანმიმდევრობა (x n ± y n ) იყრის თავს და
lim(xn ± yn) = lim xn ± lim yn;
2) თანმიმდევრობა (x n · y n ) იყრის თავს და
lim(xn · yn ) = lim xn · lim yn ;
3) თუ lim y n 6= 0, მაშინ თანაფარდობა x n /y n განისაზღვრება დაწყებული
რაღაც რიცხვი, თანმიმდევრობა ( x n ) იყრის თავს და
თეორემა 2.8 და დასკვნის მიხედვით 1, მიმდევრობები (a · βn), (b · αn), (αn · βn) უსასრულოდ მცირეა. თეორემა 2.7-ით, მიმდევრობა (aβn + bαn + αn βn ) არის უსასრულოდ მცირე. განცხადება 2) გამომდინარეობს ლემა 2.1-ის (2.5) წარმოდგენიდან.
მოდით მივმართოთ მე-3 განცხადებას). პირობით, lim yn = b 6= 0. თეორემა 2.3-ის ძალით. თანმიმდევრობა (|yn |) იყრის თავს და lim |yn | = |ბ| 6= 0. მაშასადამე, მოცემული რიცხვი ε = |b|/2, არის რიცხვი N ისეთი, რომ n > N
0 < | 2 b| = |b| −
ამიტომ, yn =6 0, და 3|b|< y n < |b| , n >ნ.
ამრიგად, xn /yn კოეფიციენტი განისაზღვრება ყველა n > N-სთვის და თანმიმდევრობა (1/yn) შეზღუდულია. განვიხილოთ ყველა n > N განსხვავება
(αn b − aβn ). |
|||||||||||||||||||||
ქვემიმდევრობა |
αn b |
aβn |
უსაზღვროდ პატარა |
||||||||||||||||||
შეზღუდული. თეორემა 2.8-ით მიმდევრობა |
|||||||||||||||||||||
− ბ |
|||||||||||||||||||||
ძალიან პატარა. მაშასადამე, ლემა 2.1, განცხადება 3) დადასტურებულია. დასკვნა 1. თუ მიმდევრობა (xn) იყრის თავს, მაშინ ნებისმიერისთვის
ნებისმიერი c რიცხვისთვის მიმდევრობა (c · xn ) იყრის თავს და lim(cxn ) = c · lim xn .
უსასრულოდ მცირე ფუნქციები
ფუნქცია %%f(x)%% გამოძახებულია უსასრულოდ მცირე(b.m.) %%x \-მდე \in \overline(\mathbb(R))%%, თუ არგუმენტის ამ ტენდენციით ფუნქციის ლიმიტი ნულის ტოლია.
ცნება ბ.მ. ფუნქცია განუყოფლად არის დაკავშირებული ინსტრუქციებთან მისი არგუმენტის შესაცვლელად. შეიძლება ვისაუბროთ ბ.მ. ფუნქციონირებს %%a \a + 0%% -ზე და %%a \a - 0%% -ზე. ჩვეულებრივ ბ.მ. ფუნქციები აღინიშნება ბერძნული ანბანის პირველი ასოებით %%\alpha, \beta, \გამა, \ldots%%
მაგალითები
- ფუნქცია %%f(x) = x%% არის b.m. %%x \ 0%%-ზე, ვინაიდან მისი ლიმიტი %%a = 0%% არის ნული. ორმხრივი ზღვრისა და ცალმხრივი ზღვრის კავშირის შესახებ თეორემის მიხედვით ეს ფუნქცია ბ.მ. ორივე %%x \ to +0%% და %%x \ to -0%%–ით.
- ფუნქცია %%f(x) = 1/(x^2)%% - ბ.მ. %%x \ to \infty%%–ზე (ასევე %%x \ to +\infty%%–ზე და %%x \ to -\infty%%)–ზე.
არანულოვანი მუდმივი რიცხვი, რაც არ უნდა მცირე იყოს აბსოლუტური მნიშვნელობით, არ არის b.m. ფუნქცია. მუდმივი რიცხვებისთვის ერთადერთი გამონაკლისი არის ნული, ვინაიდან ფუნქცია %%f(x) \equiv 0%% აქვს ნულოვანი ლიმიტი.
თეორემა
ფუნქცია %%f(x)%% აქვს გაფართოებული რიცხვითი წრფის %%a \in \overline(\mathbb(R))%% წერტილში საბოლოო ზღვარი, რომელიც ტოლია რიცხვის %%b%% თუ და მხოლოდ თუ ეს ფუნქცია უდრის ამ რიცხვის ჯამს %%b%% და ბ.მ. ფუნქციები %%\alpha(x)%% %%x \ to a%%, ან $$ \არსებობს~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \მარცხენა მარჯვენა ისარი \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \a)(\alpha(x) = 0)\right). $$
უსასრულოდ მცირე ფუნქციების თვისებები
%%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%% ზღვრამდე გადასვლის წესების მიხედვით, შემდეგი დებულებებია:
- ბ.მ-ის საბოლოო რიცხვის ჯამი. ფუნქციები %%x \ to a%% არის b.m. %%x \a%%–ზე.
- ნებისმიერი რიცხვის ნამრავლი ბ.მ. ფუნქციები %%x \ to a%% არის b.m. %%x \a%%–ზე.
პროდუქტი ბ.მ. ფუნქციონირებს %%x \a%%–ზე და ფუნქცია შემოსაზღვრულია ზოგიერთ პუნქციურ უბანში %%\stackrel(\circ)(\text(U))(a)%% a წერტილის, არის b.m. %%x \ to a%% ფუნქციაზე.
ნათელია, რომ მუდმივი ფუნქციის ნამრავლი და ბ.მ. %%x \a%%-ზე არის ბ.მ. ფუნქცია %%x \a%%–ზე.
ექვივალენტური უსასრულო მცირე ფუნქციები
უსასრულოდ მცირე ფუნქციები %%\alpha(x), \beta(x)%% %%x \ to a%% ეწოდება ექვივალენტიდა ჩაწერეთ %%\alpha(x) \sim \beta(x)%%, თუ
$$ \lim\limits_(x \a)(\frac(\alpha(x))(\beta(x)) = \lim\limits_(x \a)(\frac(\beta(x) )(\ალფა(x))) = 1. $$
თეორემა ბ.მ-ის ჩანაცვლების შესახებ. ფუნქციების ექვივალენტი
დაე, %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% იყოს b.m. ფუნქციები %%x \ to a%%, %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, შემდეგ $$ \lim\limits_(x \a)(\frac(\alpha(x))(\beta(x)) = \lim\ ლიმიტები_(x \a)(\frac(\alpha_1(x))(\beta_1(x))). $$
ეკვივალენტური ბ.მ. ფუნქციები.
დაე, %%\alpha(x)%% იყოს b.m. ფუნქცია %%x \ to a%%, შემდეგ
- %%\sin(\alpha(x)) \sim \alpha(x)%%
- %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
- %%\tan \alpha(x) \sim \alpha(x)%%
- %%\arcsin\alpha(x) \sim \alpha(x)%%
- %%\arctan\alpha(x) \sim \alpha(x)%%
- %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
- %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
- %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%
მაგალითი
$$ \begin(მასივი)(ll) \lim\limits_(x \0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \ to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \ to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \0-მდე)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(მასივი) $$
უსაზღვროდ დიდი ფუნქციები
ფუნქცია %%f(x)%% გამოძახებულია უსასრულოდ დიდი(b.b.) %%x \ to \in \overline(\mathbb(R))%%, თუ არგუმენტის ამ ტენდენციით ფუნქციას აქვს უსასრულო ზღვარი.
მსგავსი ბ.მ. ფუნქციების კონცეფცია ბ.ბ. ფუნქცია განუყოფლად არის დაკავშირებული ინსტრუქციებთან მისი არგუმენტის შესაცვლელად. შეიძლება ვისაუბროთ ბ.ბ. ფუნქციონირებს %%x \a + 0%%–ით და %%x \a - 0%%–ით. ტერმინი „უსასრულოდ დიდი“ არ საუბრობს ფუნქციის აბსოლუტურ მნიშვნელობაზე, არამედ მისი ცვლილების ბუნებაზე მოცემული წერტილის სიახლოვეს. არც ერთი მუდმივი რიცხვი, რაც არ უნდა დიდი იყოს აბსოლუტური მნიშვნელობით, არ არის უსასრულოდ დიდი.
მაგალითები
- ფუნქცია %%f(x) = 1/x%% - ბ.ბ. %%x \ 0%-მდე.
- ფუნქცია %%f(x) = x%% - b.b. %%x \ to \infty%%.
თუ განსაზღვრის პირობებია $$ \begin(მასივი)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(მასივი) $$
შემდეგ ისინი საუბრობენ დადებითიან უარყოფითიბ.ბ. %%a%% ფუნქციაზე.
მაგალითი
ფუნქცია %%1/(x^2)%% - დადებითი ბ.ბ. %%x \ 0%-მდე.
კავშირი ბ.ბ. და ბ.მ. ფუნქციები
თუ %%f(x)%% არის b.b. %%x \ to a%% ფუნქციით, შემდეგ %%1/f(x)%% - ბ.მ.
%%x \a%%–ზე. თუ %%\alpha(x)%% - ბ.მ. რადგან %%x \ to a%% არის არანულოვანი ფუნქცია %%a%% წერტილის ზოგიერთ პუნქციასთან, მაშინ %%1/\alpha(x)%% არის b.b. %%x \a%%–ზე.
უსასრულოდ დიდი ფუნქციების თვისებები
წარმოგიდგენთ b.b-ის რამდენიმე თვისებას. ფუნქციები. ეს თვისებები პირდაპირ გამომდინარეობს ბ.ბ. სასრული ზღვრების მქონე ფუნქციების ფუნქციები და თვისებები, ასევე ბ.ბ.-ს შორის კავშირის თეორემადან. და ბ.მ. ფუნქციები.
- სასრული რიცხვის ნამრავლი b.b. ფუნქციები %%x \ to a%% არის b.b. ფუნქცია %%x \a%%–ზე. მართლაც, თუ %%f_k(x), k = \overline(1, n)%% - b.b. ფუნქციონირებს %%x \ to a%%, შემდეგ წერტილის ზოგიერთ პუნქციურ მიდამოში %%a%% %%f_k(x) \ne 0%% და კავშირის თეორემით ბ.ბ. და ბ.მ.ფუნქციები %%1/f_k(x)%% - ბ.მ. ფუნქცია %%x \a%%–ზე. გამოდის %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m ფუნქცია %%x \ to a%%, და %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - ბ.ბ. ფუნქცია %%x \a%%–ზე.
- პროდუქტი ბ.ბ. ფუნქციები %%x \ to a%%–სთვის და ფუნქცია, რომელიც წერტილის %%a%% პუნქციურ მიდამოებში აბსოლუტური სიდიდით მეტია დადებით მუდმივზე არის b.b. ფუნქცია %%x \a%%–ზე. კერძოდ, პროდუქტი ბ.ბ. ფუნქცია %%x \ to a%%–ით და ფუნქცია, რომელსაც აქვს სასრული არანულოვანი ზღვარი %%a%% წერტილში იქნება b.b. ფუნქცია %%x \a%%–ზე.
ჯამი ორი ბ.ბ. ფუნქციონირებს %%x \ to a%% -ზე არის გაურკვევლობა. ტერმინების ნიშნიდან გამომდინარე, ასეთი თანხის ცვლილების ბუნება შეიძლება ძალიან განსხვავებული იყოს.
მაგალითი
მოცემული იყოს %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. ფუნქციონირებს %%x \ to \infty%%. შემდეგ:
- %%f(x) + g(x) = 3x%% - ბ.ბ. ფუნქცია %%x \ to \infty%%;
- %%f(x) + h(x) = 0%% - ბ.მ. ფუნქცია %%x \ to \infty%%;
- %%h(x) + v(x) = \sin x%% არ აქვს ლიმიტი %%x \ to \infty%%.
ფუნქციის ჯამი, რომელიც შემოსაზღვრულია %%a%% წერტილის ზოგიერთ პუნქციასთან და b.b. ფუნქციები %%x \ to a%% არის b.b. ფუნქცია %%x \a%%–ზე.
მაგალითად, ფუნქციები %%x - \sin x%% და %%x + \cos x%% არის b.b. %%x \ to \infty%%.
