Bezgalīgi mazas sekvences – definīcija un īpašības. Piemēri Kādu lielumu sauc par bezgalīgi mazu
Bezgalīgi mazo un lielo aprēķins
Bezgalīgi mazs aprēķins- aprēķini, kas veikti ar bezgalīgi maziem lielumiem, kuros atvasinātais rezultāts tiek uzskatīts par bezgalīgi mazo lielumu bezgalīgu summu. Bezgalīgi mazo skaitļu aprēķins ir vispārējs diferenciālskaitļa un integrāļa aprēķina jēdziens, kas veido mūsdienu augstākās matemātikas pamatu. Bezgalīgi maza daudzuma jēdziens ir cieši saistīts ar robežas jēdzienu.
Bezgalīgi mazs
Secība a n sauca bezgala mazs, Ja. Piemēram, skaitļu virkne ir bezgalīgi maza.
Funkcija tiek izsaukta bezgalīgi mazs punkta tuvumā x 0 ja ![]() .
.
Funkcija tiek izsaukta bezgalīgi mazs bezgalībā, Ja ![]() vai
vai ![]() .
.
Arī bezgalīgi maza ir funkcija, kas ir atšķirība starp funkciju un tās robežu, tas ir, ja ![]() , Tas f(x) − a = α( x)
, .
, Tas f(x) − a = α( x)
, .
Bezgala liels daudzums
Visās zemāk redzamajās formulās bezgalībai pa labi no vienlīdzības ir noteikta zīme (“pluss” vai “mīnuss”). Tā ir, piemēram, funkcija x grēks x, neierobežots no abām pusēm, nav bezgalīgi liels pie .
Secība a n sauca bezgala liels, Ja ![]() .
.
Funkcija tiek izsaukta bezgalīgi liels punkta tuvumā x 0 ja ![]() .
.
Funkcija tiek izsaukta bezgalīgi liels bezgalībā, Ja ![]() vai
vai ![]() .
.
Bezgalīgi maza un bezgalīgi liela īpašības
Bezgalīgi mazo lielumu salīdzinājums
Kā salīdzināt bezgalīgi mazus daudzumus?
Bezgalīgi mazo lielumu attiecība veido tā saukto nenoteiktību.
Definīcijas
Pieņemsim, ka mums ir bezgalīgi mazas vērtības α( x) un β( x) (vai, kas definīcijai nav svarīgi, bezgalīgi mazas secības).
Lai aprēķinātu šādus ierobežojumus, ir ērti izmantot L'Hopital noteikumu.
Salīdzināšanas piemēri
Izmantojot PAR-simbolisms, iegūtos rezultātus var uzrakstīt šādā formā x 5 = o(x 3). Šajā gadījumā šādi ieraksti ir patiesi: 2x 2 + 6x = O(x) Un x = O(2x 2 + 6x).Līdzvērtīgas vērtības
Definīcija
Ja , tad tiek izsaukti bezgalīgi mazi lielumi α un β ekvivalents ().
Ir skaidrs, ka ekvivalenti lielumi ir īpašs bezgalīgi mazu lielumu gadījums ar tādu pašu mazuma pakāpi.
Ja ir spēkā šādas ekvivalences attiecības (kā tā saukto ievērojamo robežu sekas):
Teorēma
Divu bezgalīgi mazu lielumu koeficienta (attiecības) robeža nemainīsies, ja vienu no tiem (vai abus) aizstās ar līdzvērtīgu lielumu.Šai teorēmai ir praktiska nozīme robežu atrašanā (sk. piemēru).
Lietošanas piemērs
Nomaiņa sin 2x ekvivalenta vērtība 2 x, saņemamVēsturiskā skice
Jēdziens “bezgalīgi mazs” tika apspriests jau senos laikos saistībā ar nedalāmo atomu jēdzienu, taču tas netika iekļauts klasiskajā matemātikā. Tas atkal tika atdzīvināts, kad 16. gadsimtā parādījās “nedalāmo metodi”, sadalot pētāmo figūru bezgalīgi mazās daļās.
17. gadsimtā notika bezgalīgi mazo skaitļu algebraizācija. Tos sāka definēt kā skaitliskus lielumus, kas ir mazāki par jebkuru galīgu (kas nav nulles) lielumu un tomēr nav vienādi ar nulli. Analīzes māksla sastāvēja no relāciju sastādīšanas, kas satur bezgalīgi mazas vērtības (diferenciāļus), un pēc tam to integrējot.
Vecās skolas matemātiķi šo koncepciju pārbaudīja bezgala mazs skarba kritika. Mišels Rolle rakstīja, ka jaunais aprēķins ir " ģeniālu kļūdu kopums"; Voltērs kaustiski atzīmēja, ka aprēķini ir māksla aprēķināt un precīzi izmērīt lietas, kuru esamību nevar pierādīt. Pat Huigenss atzina, ka viņš nesaprot augstākas pakāpes diferenciāļu nozīmi.
Par likteņa ironiju var uzskatīt nestandarta analīzes rašanos gadsimta vidū, kas pierādīja, ka arī sākotnējais skatījums - faktiskie infinitesimals - bija konsekvents un var tikt izmantots par analīzes bāzi.
Skatīt arī
Wikimedia fonds. 2010. gads.
Skatiet, kas ir “bezgalīgi mazs daudzums” citās vārdnīcās:
BEZERĒGI MAZS DAUDZUMS- mainīgs lielums noteiktā procesā, ja šajā procesā tas bezgalīgi tuvojas (tiecas) uz nulli... Lielā Politehniskā enciklopēdija
Bezgalīgi mazs- ■ Kaut kas nezināms, bet saistīts ar homeopātiju... Kopējo patiesību leksikons
BEZGALĪGI MAZAS FUNKCIJAS UN TO PAMATĪPAŠĪBAS
Funkcija y=f(x) sauca bezgala mazs plkst x→a vai kad x→∞, ja vai , t.i. bezgalīgi maza funkcija ir funkcija, kuras robeža noteiktā punktā ir nulle.
Piemēri.
Nodibināsim šādas svarīgas attiecības:
Teorēma. Ja funkcija y=f(x) reprezentējams ar x→a kā nemainīga skaitļa summa b un bezgalīgi mazs lielums α(x): f(x)=b+ α(x) Tas .
Un otrādi, ja , tad f(x)=b+α(x), Kur a(x)– bezgalīgi mazs plkst x→a.
Pierādījums.
Apskatīsim bezgalīgi mazo funkciju pamatīpašības.
1. teorēma. Divu, trīs un vispār jebkura ierobežota bezgalīgi mazo lielumu algebriskā summa ir bezgalīgi maza funkcija.
Pierādījums. Sniegsim pierādījumu diviem terminiem. Ļaujiet f(x)=α(x)+β(x), kur un . Mums ir jāpierāda, ka jebkuram patvaļīgi mazam ε > 0 atrasts δ> 0, piemēram, par x, apmierinot nevienlīdzību |x – a|<δ , veikta |f(x)|< ε.
Tātad, nofiksēsim patvaļīgu skaitli ε > 0. Tā kā saskaņā ar teorēmas nosacījumiem α(x) ir bezgalīgi maza funkcija, tad ir tāda δ 1 > 0, kas ir |x – a|< δ 1 mums ir |α(x)|< ε / 2. Tāpat kopš β(x) ir bezgalīgi mazs, tad ir tāds δ 2 > 0, kas ir |x – a|< δ 2 mums ir | β(x)|< ε / 2.
Ņemsim δ=min(δ 1 , δ2 } .Tad punkta tuvumā a rādiuss δ tiks apmierināta katra no nevienādībām |α(x)|< ε / 2 un | β(x)|< ε / 2. Tāpēc šajā apkaimē būs
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
tie. |f(x)|< ε, kas bija jāpierāda.
2. teorēma. Bezgalīgi mazas funkcijas reizinājums a(x) ierobežotai funkcijai f(x) plkst x→a(vai kad x→∞) ir bezgalīgi maza funkcija.
Pierādījums. Kopš funkcijas f(x) ir ierobežots, tad ir skaits M tāds, ka visām vērtībām x no kāda punkta apkārtnes a|f(x)|≤M. Turklāt kopš a(x) ir bezgalīgi maza funkcija pie x→a, tad patvaļīgam ε > 0 ir punkta apkārtne a, kurā pastāvēs nevienlīdzība |α(x)|< ε /M. Tad mazākajā no šiem rajoniem, kas mums ir | αf|< ε /M= ε. Un tas nozīmē to af- bezgalīgi mazs. Šim gadījumam x→∞ pierādīšana tiek veikta līdzīgi.
No pārbaudītās teorēmas izriet:
Secinājums 1. Ja un, tad.
Secinājums 2. Ja c= const, tad .
3. teorēma. Bezgalīgi mazas funkcijas attiecība α(x) pēc funkcijas f(x), kuras robeža atšķiras no nulles, ir bezgalīgi maza funkcija.
Pierādījums. Ļaujiet ![]() . Tad 1 /f(x) ir ierobežota funkcija. Tāpēc frakcija
. Tad 1 /f(x) ir ierobežota funkcija. Tāpēc frakcija ![]() ir bezgalīgi mazas funkcijas un ierobežotas funkcijas reizinājums, t.i. funkcija ir bezgalīgi maza.
ir bezgalīgi mazas funkcijas un ierobežotas funkcijas reizinājums, t.i. funkcija ir bezgalīgi maza.
BEZGALĪGI MAZĀM UN BEZGALĪGI LIELĀM FUNKCIJĀM ATTIECĪBAS
1. teorēma. Ja funkcija f(x) ir bezgalīgi liels plkst x→a, tad funkcija 1 /f(x) ir bezgalīgi mazs plkst x→a.
Pierādījums.Ņemsim patvaļīgu skaitli ε >0 un parādīt to dažiem δ>0 (atkarībā no ε) visiem x, par kuru |x – a|<δ , nevienlīdzība ir apmierināta, un tas to nozīmēs 1/f(x) ir bezgalīgi maza funkcija. Patiešām, kopš f(x) ir bezgalīgi liela funkcija pie x→a, tad būs δ>0 tāda, ka tiklīdz |x – a|<δ , tātad | f(x)|> 1/ ε. Bet tad par to pašu x.
Piemēri.
Var pierādīt arī apgriezto teorēmu.
2. teorēma. Ja funkcija f(x)- bezgalīgi mazs plkst x→a(vai x→∞) un tad nepazūd y= 1/f(x) ir bezgala liela funkcija.
Veiciet teorēmas pierādīšanu pats.
Piemēri.
Tādējādi bezgalīgi mazu un bezgalīgi lielu funkciju vienkāršākās īpašības var uzrakstīt, izmantojot šādas nosacītās attiecības: A≠ 0
ROBEŽA TEOREMAS
1. teorēma. Divu, trīs un vispār noteikta skaita funkciju algebriskās summas robeža ir vienāda ar šo funkciju robežu algebrisko summu, t.i.
Pierādījums. Pierādīšanu veiksim diviem terminiem, jo to var izdarīt vienādi jebkuram terminu skaitam. Ļaujiet ![]() .Tad f(x)=b+α(x) Un g(x)=c+β(x), Kur α
Un β
– bezgalīgi mazas funkcijas. Tāpēc
.Tad f(x)=b+α(x) Un g(x)=c+β(x), Kur α
Un β
– bezgalīgi mazas funkcijas. Tāpēc
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Jo b+c ir konstante, un α(x) + β(x) tad ir bezgalīgi maza funkcija
Piemērs. .
2. teorēma. Divu, trīs un parasti ierobežota skaita funkciju reizinājuma robeža ir vienāda ar šo funkciju robežu reizinājumu:
Pierādījums. Ļaujiet ![]() . Tāpēc f(x)=b+α(x) Un g(x)=c+β(x) Un
. Tāpēc f(x)=b+α(x) Un g(x)=c+β(x) Un
fg = (b + α) (c + β) = bc + (bβ + cα + αβ).
Darbs bc ir nemainīga vērtība. Funkcija bβ + c α + αβ pamatojoties uz bezgalīgi mazo funkciju īpašībām, ir bezgalīgi mazs daudzums. Tāpēc .
Secinājums 1. Pastāvīgo koeficientu var ņemt aiz robežzīmes:
![]() .
.
Secinājums 2. Pakāpes ierobežojums ir vienāds ar robežpakāpi:
![]() .
.
Piemērs.![]() .
.
3. teorēma. Divu funkciju koeficienta robeža ir vienāda ar šo funkciju robežu koeficientu, ja saucēja robeža atšķiras no nulles, t.i.
 .
.
Pierādījums. Ļaujiet . Tāpēc f(x)=b+α(x) Un g(x)=c+β(x), Kur α, β - bezgalīgi mazs. Apskatīsim koeficientu
Daļa ir bezgalīgi maza funkcija, jo skaitītājs ir bezgalīgi maza funkcija un saucējam ir ierobežojums c 2 ≠0.
Piemēri.

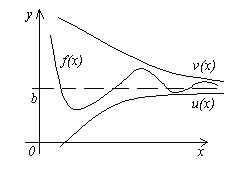
4. teorēma. Dotas trīs funkcijas f(x), u(x) Un v(x), apmierinot nevienlīdzību u (x)≤f(x)≤ v(x). Ja funkcijas u(x) Un v(x) ir tāds pats ierobežojums plkst x→a(vai x→∞), tad funkcija f(x) tiecas uz to pašu robežu, t.i. Ja
![]() , Tas.
, Tas.
Šīs teorēmas nozīme ir skaidra no attēla.
4. teorēmas pierādījums ir atrodams, piemēram, mācību grāmatā: Piskunov N. S. Diferenciālrēķins un integrālrēķins, 1. sēj. - M.: Nauka, 1985.
5. teorēma. Ja plkst x→a(vai x→∞) funkcija y=f(x) pieņem nenegatīvas vērtības y≥0 un tajā pašā laikā tiecas uz robežu b, tad šis ierobežojums nevar būt negatīvs: b ≥0.
Pierādījums. Mēs veiksim pierādīšanu ar pretrunu. Izliksimies tā b<0 , Tad |y – b|≥|b| un tāpēc starpības modulim nav tendence uz nulli, kad x→a. Bet tad y nesasniedz robežu b plkst x→a, kas ir pretrunā teorēmas nosacījumiem.
6. teorēma. Ja divas funkcijas f(x) Un g(x) visām argumenta vērtībām x apmierināt nevienlīdzību f(x)≥ g(x) un ir robežas, tad nevienlīdzība pastāv b≥c.
Pierādījums. Atbilstoši teorēmas nosacījumiem f(x)-g(x) ≥0, tāpēc pēc 5. teorēmas ![]() , vai
, vai ![]() .
.
VIENPĀRĒJIE IEROBEŽOJUMI

Līdz šim esam apsvēruši iespēju noteikt funkcijas robežu, kad x→a patvaļīgā veidā, t.i. funkcijas ierobežojums nebija atkarīgs no tā, kā tā tika novietota x virzienā a, pa kreisi vai pa labi no a. Tomēr diezgan bieži tiek atrastas funkcijas, kurām šajā nosacījumā nav ierobežojumu, taču tām ir ierobežojums, ja x→a, kas paliek vienā pusē A, pa kreisi vai pa labi (skat. attēlu). Tāpēc tiek ieviesti vienpusējo ierobežojumu jēdzieni.
Ja f(x) tiecas līdz robežai b plkst x tiecas uz noteiktu skaitu a Tātad x pieņem tikai vērtības, kas ir mazākas par a, tad viņi raksta un zvana funkcijas f(x) robeža punktā a pa kreisi.
Bezgalīgi mazo un lielo aprēķins
Bezgalīgi mazs aprēķins- aprēķini, kas veikti ar bezgalīgi maziem lielumiem, kuros atvasinātais rezultāts tiek uzskatīts par bezgalīgi mazo lielumu bezgalīgu summu. Bezgalīgi mazo skaitļu aprēķins ir vispārējs diferenciālskaitļa un integrāļa aprēķina jēdziens, kas veido mūsdienu augstākās matemātikas pamatu. Bezgalīgi maza daudzuma jēdziens ir cieši saistīts ar robežas jēdzienu.
Bezgalīgi mazs
Secība a n sauca bezgala mazs, Ja. Piemēram, skaitļu virkne ir bezgalīgi maza.
Funkcija tiek izsaukta bezgalīgi mazs punkta tuvumā x 0 ja ![]() .
.
Funkcija tiek izsaukta bezgalīgi mazs bezgalībā, Ja ![]() vai
vai ![]() .
.
Arī bezgalīgi maza ir funkcija, kas ir atšķirība starp funkciju un tās robežu, tas ir, ja ![]() , Tas f(x) − a = α( x)
, .
, Tas f(x) − a = α( x)
, .
Bezgala liels daudzums
Secība a n sauca bezgala liels, Ja ![]() .
.
Funkcija tiek izsaukta bezgalīgi liels punkta tuvumā x 0 ja ![]() .
.
Funkcija tiek izsaukta bezgalīgi liels bezgalībā, Ja ![]() vai
vai ![]() .
.
Visos gadījumos bezgalībai uz vienlīdzības tiesībām tiek domāta noteikta zīme (“pluss” vai “mīnuss”). Tā ir, piemēram, funkcija x grēks x nav bezgalīgi liels pie .
Bezgalīgi maza un bezgalīgi liela īpašības
Bezgalīgi mazo lielumu salīdzinājums
Kā salīdzināt bezgalīgi mazus daudzumus?
Bezgalīgi mazo lielumu attiecība veido tā saukto nenoteiktību.
Definīcijas
Pieņemsim, ka mums ir bezgalīgi mazas vērtības α( x) un β( x) (vai, kas definīcijai nav svarīgi, bezgalīgi mazas secības).
Lai aprēķinātu šādus ierobežojumus, ir ērti izmantot L'Hopital noteikumu.
Salīdzināšanas piemēri
Izmantojot PAR-simbolisms, iegūtos rezultātus var uzrakstīt šādā formā x 5 = o(x 3). Šajā gadījumā šādi ieraksti ir patiesi: 2x 2 + 6x = O(x) Un x = O(2x 2 + 6x).Līdzvērtīgas vērtības
Definīcija
Ja , tad tiek izsaukti bezgalīgi mazi lielumi α un β ekvivalents ().
Ir skaidrs, ka ekvivalenti lielumi ir īpašs bezgalīgi mazu lielumu gadījums ar tādu pašu mazuma pakāpi.
Ja ir spēkā šādas ekvivalences attiecības: , , ![]() .
.
Teorēma
Divu bezgalīgi mazu lielumu koeficienta (attiecības) robeža nemainīsies, ja vienu no tiem (vai abus) aizstās ar līdzvērtīgu lielumu.Šai teorēmai ir praktiska nozīme robežu atrašanā (sk. piemēru).
Lietošanas piemērs
Nomaiņa sin 2x ekvivalenta vērtība 2 x, saņemamVēsturiskā skice
Jēdziens “bezgalīgi mazs” tika apspriests jau senos laikos saistībā ar nedalāmo atomu jēdzienu, taču tas netika iekļauts klasiskajā matemātikā. Tas atkal tika atdzīvināts, kad 16. gadsimtā parādījās “nedalāmo metodi”, sadalot pētāmo figūru bezgalīgi mazās daļās.
17. gadsimtā notika bezgalīgi mazo skaitļu algebraizācija. Tos sāka definēt kā skaitliskus lielumus, kas ir mazāki par jebkuru galīgu (kas nav nulles) lielumu un tomēr nav vienādi ar nulli. Analīzes māksla sastāvēja no relāciju sastādīšanas, kas satur bezgalīgi mazas vērtības (diferenciāļus), un pēc tam to integrējot.
Vecās skolas matemātiķi šo koncepciju pārbaudīja bezgala mazs skarba kritika. Mišels Rolle rakstīja, ka jaunais aprēķins ir " ģeniālu kļūdu kopums"; Voltērs kaustiski atzīmēja, ka aprēķini ir māksla aprēķināt un precīzi izmērīt lietas, kuru esamību nevar pierādīt. Pat Huigenss atzina, ka viņš nesaprot augstākas pakāpes diferenciāļu nozīmi.
Strīdi Parīzes Zinātņu akadēmijā par analīzes pamatojumu kļuva tik skandalozi, ka akadēmija savulaik pilnībā aizliedza saviem biedriem runāt par šo tēmu (tas galvenokārt attiecās uz Rolu un Varinjonu). 1706. gadā Rolle publiski atsauca savus iebildumus, bet diskusijas turpinājās.
1734. gadā slavenais angļu filozofs bīskaps Džordžs Bērklijs publicēja sensacionālu brošūru, kas pazīstama ar saīsinātu nosaukumu “ Analītiķis" Tās pilns nosaukums: " Analītiķis jeb diskurss, kas adresēts neticīgajam matemātiķim, jautājot, vai mūsdienu analīzes priekšmets, principi un secinājumi ir skaidrāk uztverami vai skaidrāk izsecināmi nekā reliģiskie noslēpumi un ticības apliecības.».
Analītiķis saturēja asprātīgu un lielākoties godīgu kritiku par bezgalīgi maziem aprēķiniem. Bērklijs uzskatīja, ka analīzes metode neatbilst loģikai un rakstīja, ka " lai cik noderīgs tas būtu, to var uzskatīt tikai par sava veida minējumu; izveicīga prasme, māksla vai drīzāk triks, bet ne kā zinātniska pierādīšanas metode" Citējot Ņūtona frāzi par pašreizējo daudzumu pieaugumu “pašā to rašanās vai izzušanas sākumā”, Bērklijs ironiski: “ tie nav ne galīgi lielumi, ne bezgalīgi mazi, ne pat nekas. Vai mēs nevaram tos saukt par mirušo lielumu rēgiem?... Un kā vispār var runāt par attiecībām starp lietām, kurām nav lieluma?.. Ikviens, kurš spēj sagremot otro vai trešo fluxion [atvasinājumu], otro vai trešo atšķirība, nevajadzētu, jo man šķiet, ka teoloģijā kaut kas jāmeklē».
Bērklijs raksta, ka nav iespējams iedomāties momentāno ātrumu, tas ir, ātrumu noteiktā mirklī un noteiktā punktā, jo kustības jēdziens ietver (galīgas nulles līmeņa) telpas un laika jēdzienus.
Kā analīze dod pareizus rezultātus? Bērklijs nonāca pie domas, ka tas izskaidrojams ar vairāku kļūdu klātbūtni analītiskos secinājumos, un ilustrēja to ar parabolas piemēru. Interesanti, ka daži galvenie matemātiķi (piemēram, Lagranžs) viņam piekrita.
Radās paradoksāla situācija, kad stingrība un auglība matemātikā traucēja viens otram. Neskatoties uz nelikumīgu darbību izmantošanu ar slikti definētiem jēdzieniem, tiešu kļūdu skaits bija pārsteidzoši mazs - intuīcija nāca palīgā. Un tomēr visā 18. gadsimtā matemātiskā analīze strauji attīstījās bez būtības nekāda pamatojuma. Tā efektivitāte bija pārsteidzoša un runāja pati par sevi, taču diferenciāļa nozīme joprojām bija neskaidra. Īpaši bieži tika sajaukts funkcijas bezgalīgi mazais pieaugums un tās lineārā daļa.
Visā 18. gadsimtā tika pieliktas milzīgas pūles, lai situāciju labotu, un tajās piedalījās gadsimta labākie matemātiķi, taču tikai Košī 19. gadsimta sākumā izdevās pārliecinoši izveidot analīzes pamatu. Viņš stingri definēja pamatjēdzienus - robeža, konverģence, nepārtrauktība, diferenciālis utt., pēc kuriem faktiskie bezgalīgi mazie pazuda no zinātnes. Daži atlikušie smalkumi tika paskaidroti vēlāk
Teorēma 2.4. Ja secības (x n) un (y n) saplūst un x n ≤ y n, n > n 0, tad lim x n ≤ lim y n.
Lai lim xn = a, |
lim yn = b un a > b. Pēc definīcijas 2.4 ierobežojumi |
||||||||||||||||||||
secības pēc skaitļa ε = |
ir tāds skaitlis N |
||||||||||||||||||||
Tāpēc n > max(n0 , N) yn< |
< xn , что противоречит |
||||||||||||||||||||
stāvokli. |
|||||||||||||||||||||
komentēt. Ja secības (xn), (yn) saplūst |
|||||||||||||||||||||
visi n > n0 |
xn< yn , то можно утверждать лишь, что lim xn |
≤ lim yn . |
|||||||||||||||||||
Lai to redzētu, pietiek apsvērt secības
un yn = |
||||
No 2.4. definīcijas tieši izriet šādi rezultāti.
Teorēma 2.5. Ja skaitļu secība (x n) saplūst un lim x n< b (b R), то N N: x n < b, n >N.
Sekas. Ja secība (xn) saplūst un lim xn 6= 0, tad
N N: sgn xn = sgn(lim xn), n > N.
Teorēma 2.6. Ļaujiet sekvencēm (x n), (y n), (z n) izpildīt nosacījumus:
1) x n ≤ yn ≤ zn, n > n0,
2) sekvences(x n) un (z n) saplūst un lim x n = lim z n = a.
Tad secība (y n ) saplūst un lim y n = a.
2.1.3 Bezgalīgi mazas secības
Definīcija 2.7. Skaitļu secību (x n) sauc par bezgalīgi mazu (bezgalīgi mazu), ja tā saplūst un lim x n = 0.
Saskaņā ar skaitļu virknes ierobežojumu 2.4. definīciju 2.7. definīcija ir līdzvērtīga šādai:
Definīcija 2.8. Skaitļu secību (x n) sauc par bezgalīgi mazu, ja jebkuram pozitīvam skaitlim ε ir tāds skaitlis N = N(ε), ka visiem n > N šīs secības elementi x n apmierina nevienādību |x n |< ε.
Tātad, (xn) - b.m. ε > 0 N = N(ε) : n > N |xn |< ε.
No 2., 3. piemēra un 1. piezīmes līdz 2.3. teorēmai mēs iegūstam, ka pēc
derīgums ( |
q−n |
ir bezgalīgi |
||||||||||||
Bezgalīgi mazo secību īpašības apraksta šādas teorēmas.
Teorēma 2.7. Galīga skaita bezgalīgi mazu secību summa ir bezgalīgi maza secība.
Lai secības (xn), (yn) ir bezgalīgi mazas. Parādīsim, ka (xn + yn) arī būs viens. Uzstādām ε > 0. Tad ir skaitlis
N1 = N1 (ε) tā, ka |
||||
|xn |< |
N>N1, |
|||
un ir tāds skaitlis N2 = N2 (ε), ka |
||||
|yn |< |
N>N2. |
|||
Apzīmēsim ar N = max(N1, N2). Ja n > N, būs spēkā nevienādības (2.1) un (2.2). Tāpēc n > N
|xn + yn | ≤ |xn | + |yn |< 2 + 2 = ε.
Tas nozīmē, ka secība (xn +yn) ir bezgalīgi maza. Paziņojums par ierobežota skaita bezgalīgi mazu secību summu
Tas izriet no tā, kas tika pierādīts ar indukciju.
Teorēma 2.8. Bezgalīgi mazas secības un ierobežotas secības reizinājums ir bezgalīgi mazs.
Lai (xn) ir ierobežota un (yn) ir bezgalīgi maza secība. Saskaņā ar 2.6. definīciju ierobežotai secībai ir tāds skaitlis M > 0, ka
|xn | ≤ M, n N. |
Nofiksēsim patvaļīgu skaitli ε > 0. Tā kā (yn ) ir bezgalīgi maza secība, ir tāds skaitlis N = N(ε), ka
Tāpēc secība (xn yn ) ir bezgalīgi mazs.

Secinājums 1. Bezgalīgi mazas un konverģentas secības reizinājums ir bezgalīgi maza secība.
Secinājums 2. Divu bezgalīgi mazu secību reizinājums ir bezgalīgi maza secība.
Izmantojot bezgalīgi mazas sekvences, konverģentas secības definīciju var aplūkot dažādi.
Lemma 2.1. Lai skaitlis a būtu skaitliskās secības (x n) robeža, ir nepieciešams un pietiekami, lai būtu attēlojums x n = a + α n, n N, kurā (α n) ir bezgalīgi maza secība.
Nepieciešamība. Lai lim xn = a un a R. Tad
ε > 0 N = N(ε) N: n > N |xn − a|< ε.
Ja mēs uzstādām αn = xn − a, n N, tad iegūstam, ka (αn) ir bezgalīgi maza secība un xn = a + αn, n N.
Atbilstība. Lai secība (xn) būtu tāda, ka eksistē skaitlis a, kuram xn = a + αn, n N un lim αn = 0. Fiksēsim patvaļīgu pozitīvu skaitli ε. Tā kā lim αn = 0, tad ir tāds skaitlis N = N(ε) N, ka |αn |< ε, n >N. Tas ir, citos apzīmējumos n > N |xn − a|< ε. Это означает, что lim xn = a.
Piemērosim Lemmu 2.1 svarīgam konkrētam piemēram.
Lemma 2.2. lim n n = 1.
√ √
Tā kā visiem n > 1 n n > 1, tad n n = 1 + αn un αn > 0
visi n > 1. Tāpēc n = (1 + α |
)n = 1 + nα |
+ αn. |
|||||||||||||||
Tā kā visi termini ir pozitīvi, n |
|||||||||||||||||
Lai ε > 0. Kopš |
2/n< ε для всех n >2/ε , tad, pieņemot |
||||||||||||||||
N = max(1, ), mēs iegūstam, ka 0< αn < ε, n >N. Tāpēc
secība (αn) ir bezgalīgi maza un saskaņā ar lemmu
2,1, lim n n = 1. √
Sekas. Ja a > 1, tad lim n a = 1.√ √
Šis apgalvojums izriet no 1. nevienlīdzības< n a ≤ n n , n >[a].
2.1.4. Aritmētiskās darbības ar secībām
Izmantojot lemmu 2.1 un bezgalīgi mazo secību īpašības, ir viegli iegūt teorēmas par sekvenču robežām, kas iegūtas, izmantojot aritmētiskās darbības no konverģentām sekvencēm.

|b| 3|b|
2 < |y n | < 2
Teorēma 2.9. Ļaujiet skaitļu sekvencēm (x n) un (y n) saplūst. Tad spēkā ir šādi apgalvojumi:
1) secība (x n ± y n ) saplūst un
lim(xn ± yn) = lim xn ± lim yn;
2) secība (x n · y n ) saplūst un
lim(xn · yn ) = lim xn · lim yn ;
3) ja lim y n 6= 0, tad attiecība x n /y n tiek definēta sākot no
kādu skaitli, secība ( x n ) saplūst un
Saskaņā ar 2.8. teorēmu un 1. secinājumu secības (a · βn), (b · αn), (αn · βn) ir bezgalīgi mazas. Saskaņā ar 2.7. teorēmu secība (aβn + bαn + αn βn ) ir bezgalīgi maza. 2. apgalvojums izriet no attēlojuma (2.5) ar lemmu 2.1.
Pievērsīsimies 3. apgalvojumam). Pēc nosacījuma lim yn = b 6= 0. Saskaņā ar teorēmu 2.3. secība (|yn |) saplūst un lim |yn | = |b| 6= 0. Tāpēc, ņemot vērā skaitli ε = |b|/2, ir tāds skaitlis N, ka n > N
0 < | 2 b| = |b| −
Tāpēc yn =6 0 un 3|b|< y n < |b| , n >N.
Tādējādi koeficients xn /yn ir definēts visiem n > N, un secība (1/yn) ir ierobežota. Apsveriet visu n > N atšķirību
(αn b − aβn ). |
|||||||||||||||||||||
Secība |
αn b |
aβn |
Bezgala mazs |
||||||||||||||||||
ierobežots. Pēc 2.8. teorēmas secība |
|||||||||||||||||||||
− b |
|||||||||||||||||||||
ļoti mazs. Tāpēc ar lemmu 2.1 ir pierādīts apgalvojums 3). Secinājums 1. Ja secība (xn) saplūst, tad jebkurai
Jebkuram ciparam c secība (c · xn ) saplūst un lim(cxn ) = c · lim xn .
Bezgalīgi mazas funkcijas
Tiek izsaukta funkcija %%f(x)%%. bezgala mazs(b.m.) ar %%x \to a \in \overline(\mathbb(R))%%, ja ar šo argumenta tendenci funkcijas robeža ir vienāda ar nulli.
Jēdziens b.m. funkcija ir nesaraujami saistīta ar norādījumiem mainīt tās argumentu. Varam runāt par b.m. darbojas no %%a \līdz + 0%% un no %%a \līdz - 0%%. Parasti b.m. funkcijas ir apzīmētas ar grieķu alfabēta pirmajiem burtiem %%\alpha, \beta, \gamma, \ldots%%
Piemēri
- Funkcija %%f(x) = x%% ir b.m. pie %%x \līdz 0%%, jo tā robeža punktā %%a = 0%% ir nulle. Saskaņā ar teorēmu par saistību starp abpusējo robežu un vienpusējo robežu šī funkcija ir b.m. gan ar %%x \līdz +0%%, gan ar %%x \līdz -0%%.
- Funkcija %%f(x) = 1/(x^2)%% - b.m. %%x \līdz \infty%% (kā arī %%x \līdz +\infty%% un %%x \līdz -\infty%%).
Konstants skaitlis, kas nav nulle, neatkarīgi no tā, cik mazs ir absolūtā vērtībā, nav b.m. funkciju. Konstantiem skaitļiem vienīgais izņēmums ir nulle, jo funkcijai %%f(x) \equiv 0%% ir nulles ierobežojums.
Teorēma
Funkcijai %%f(x)%% paplašinātās skaitļu līnijas punktā %%a \in \overline(\mathbb(R))%% ir galīgais ierobežojums, kas vienāds ar skaitli %%b%% tad un tikai ja šī funkcija ir vienāda ar šī skaitļa summu %%b%% un b.m. funkcijas %%\alpha(x)%% ar %%x \to a%%, vai $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Kreisā labā bultiņa \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\right). $$
Bezgalīgi mazo funkciju īpašības
Saskaņā ar noteikumiem par pāreju uz robežu ar %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, seko šādi apgalvojumi:
- B.m gala skaita summa. funkcijas %%x \to a%% ir b.m. pie %%x \līdz a%%.
- Jebkura skaitļa reizinājums b.m. funkcijas %%x \to a%% ir b.m. pie %%x \līdz a%%.
Produkts b.m. funkcijas %%x \līdz a%% un funkcija, kas ir ierobežota kādā caurdurtajā apkārtnē %%\stackrel(\circ)(\text(U))(a)%% no punkta a, ir b.m. pie %%x \to a%% funkcija.
Ir skaidrs, ka nemainīgas funkcijas reizinājums un b.m. pie %%x \līdz a%% ir b.m. funkcija no %%x \līdz a%%.
Ekvivalentas bezgalīgi mazas funkcijas
Tiek izsauktas bezgalīgi mazas funkcijas %%\alpha(x), \beta(x)%% priekš %%x \to a%% ekvivalents un ierakstiet %%\alpha(x) \sim \beta(x)%%, ja
$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alpha(x))) = 1. $$
Teorēma par b.m aizstāšanu. funkcijas līdzvērtīgas
Lai %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% ir b.m. funkcijas %%x \to a%%, ar %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, tad $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ limits_(x \to a)(\frac(\alpha_1(x))(\beta_1(x))). $$
Ekvivalents b.m. funkcijas.
Lai %%\alpha(x)%% ir b.m. funkcija no %%x \līdz a%%, tad
- %%\sin(\alpha(x)) \sim \alpha(x)%%
- %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
- %%\tan \alpha(x) \sim \alpha(x)%%
- %%\arcsin\alpha(x) \sim \alpha(x)%%
- %%\arctan\alpha(x) \sim \alpha(x)%%
- %%\ln(1 + \alpha(x)) \sim \alpha(x)%%
- %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
- %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%
Piemērs
$$ \begin(masīvs)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(masīvs) $$
Bezgalīgi lielas funkcijas
Tiek izsaukta funkcija %%f(x)%%. bezgala liels(b.b.) ar %%x \to a \in \overline(\mathbb(R))%%, ja ar šo argumenta tendenci funkcijai ir bezgalīgs ierobežojums.
Līdzīgi kā b.m. funkciju jēdziens b.b. funkcija ir nesaraujami saistīta ar norādījumiem mainīt tās argumentu. Varam runāt par b.b. funkcijas %%x \līdz + 0%% un %%x \līdz - 0%%. Jēdziens “bezgalīgi liels” nerunā par funkcijas absolūto vērtību, bet gan par tās izmaiņu raksturu attiecīgā punkta tuvumā. Neviens konstants skaitlis, lai cik liels absolūtā vērtībā būtu, nav bezgalīgi liels.
Piemēri
- Funkcija %%f(x) = 1/x%% - b.b. pie %%x \līdz 0%%.
- Funkcija %%f(x) = x%% - b.b. pie %%x \līdz \infty%%.
Ja definīcijas nosacījumi $$ \begin(masīvs)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(masīvs) $$
tad viņi runā par pozitīvs vai negatīvs b.b. pie %%a%% funkcijas.
Piemērs
Funkcija %%1/(x^2)%% — pozitīva b.b. pie %%x \līdz 0%%.
Saikne starp b.b. un b.m. funkcijas
Ja %%f(x)%% ir b.b. ar funkciju %%x \to a%%, pēc tam %%1/f(x)%% - b.m.
pie %%x \līdz a%%. Ja %%\alpha(x)%% - b.m. priekš %%x \to a%% ir funkcija, kas nav nulle kādā punkta %%a%% caurdurtajā apkārtnē, tad %%1/\alpha(x)%% ir b.b. pie %%x \līdz a%%.
Bezgala lielu funkciju īpašības
Piedāvāsim vairākas b.b. īpašības. funkcijas. Šīs īpašības izriet tieši no b.b definīcijas. funkcijas un funkciju īpašības ar ierobežotām robežām, kā arī no teorēmas par saistību starp b.b. un b.m. funkcijas.
- Galīga skaita b.b reizinājums. funkcijas %%x \to a%% ir b.b. funkcija no %%x \līdz a%%. Patiešām, ja %%f_k(x), k = \overline(1, n)%% - b.b. funkcija no %%x \līdz a%%, tad kādā caurdurtajā apkārtnē punktam %%a%% %%f_k(x) \ne 0%% un pēc savienojuma teorēmas b.b. un b.m. funkcijas %%1/f_k(x)%% - b.m. funkcija no %%x \līdz a%%. Izrādās %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m funkcija %%x \to a%%, un %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funkcija no %%x \līdz a%%.
- Produkts b.b. funkcijas %%x \līdz a%%, un funkcija, kas kādā punkta %%a%% caurdurtajā apkārtnē absolūtā vērtībā ir lielāka par pozitīvu konstanti, ir b.b. funkcija no %%x \līdz a%%. Jo īpaši produkts b.b. funkcija ar %%x \līdz a%% un funkcija, kurai ir ierobežots, kas nav nulles robeža punktā %%a%%, būs b.b. funkcija no %%x \līdz a%%.
Divu summa b.b. funkcijas %%x \līdz a%%, pastāv nenoteiktība. Atkarībā no terminu zīmes šādas summas izmaiņu raksturs var būt ļoti atšķirīgs.
Piemērs
Dotas funkcijas %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. darbojas no %%x \līdz \infty%%. Pēc tam:
- %%f(x) + g(x) = 3x%% - b.b. funkcija %%x \to \infty%%;
- %%f(x) + h(x) = 0%% - b.m. funkcija %%x \to \infty%%;
- %%h(x) + v(x) = \sin x%% nav ierobežojumu no %%x \līdz \infty%%.
Funkcijas summa, kas robežojas ar punktu %%a%% un b.b kādā caurdurtajā apkārtnē. funkcijas ar %%x \to a%% ir b.b. funkcija no %%x \līdz a%%.
Piemēram, funkcijas %%x - \sin x%% un %%x + \cos x%% ir b.b. pie %%x \līdz \infty%%.
