Ciągi nieskończenie małe – definicja i właściwości. Przykłady Jaką wielkość nazywamy nieskończenie małą
Rachunek nieskończenie małych i dużych
Nieskończenie mały rachunek różniczkowy- obliczenia wykonywane na wielkościach nieskończenie małych, w których otrzymany wynik traktuje się jako nieskończoną sumę nieskończenie małych. Rachunek nieskończenie małych jest ogólną koncepcją rachunku różniczkowego i całkowego, która stanowi podstawę współczesnej matematyki wyższej. Pojęcie nieskończenie małej ilości jest ściśle powiązane z pojęciem granicy.
Nieskończenie mały
Podciąg A N zwany nieskończenie mały, Jeśli . Na przykład ciąg liczb jest nieskończenie mały.
Funkcja nazywa się nieskończenie małe w pobliżu punktu X 0 jeśli ![]() .
.
Funkcja nazywa się nieskończenie małe w nieskończoności, Jeśli ![]() Lub
Lub ![]() .
.
Nieskończenie mała jest także funkcja będąca różnicą między funkcją a jej granicą, to znaczy jeśli ![]() , To F(X) − A = α( X)
, .
, To F(X) − A = α( X)
, .
Nieskończenie duża ilość
We wszystkich poniższych wzorach zakłada się, że nieskończoność po prawej stronie równości ma określony znak (albo „plus”, albo „minus”). To jest na przykład funkcja X grzech X, nieograniczony po obu stronach, nie jest nieskończenie duży w .
Podciąg A N zwany nieskończenie duży, Jeśli ![]() .
.
Funkcja nazywa się nieskończenie duża w pobliżu punktu X 0 jeśli ![]() .
.
Funkcja nazywa się nieskończenie duży w nieskończoności, Jeśli ![]() Lub
Lub ![]() .
.
Własności nieskończenie małe i nieskończenie duże
Porównanie wielkości nieskończenie małych
Jak porównać nieskończenie małe ilości?
Stosunek wielkości nieskończenie małych tworzy tzw. niepewność.
Definicje
Załóżmy, że mamy nieskończenie małe wartości α( X) i β( X) (lub, co nie jest istotne dla definicji, ciągi nieskończenie małe).
Aby obliczyć takie granice, wygodnie jest skorzystać z reguły L'Hopitala.
Przykłady porównawcze
Za pomocą O-symbolizm, uzyskane wyniki można zapisać w następującej formie X 5 = o(X 3). W tym przypadku prawdziwe są następujące wpisy: 2X 2 + 6X = O(X) I X = O(2X 2 + 6X).Równoważne wartości
Definicja
Jeśli , to nazywa się nieskończenie małe wielkości α i β równowartość ().
Jest oczywiste, że ilości równoważne są szczególnym przypadkiem nieskończenie małych ilości tego samego rzędu małości.
Gdy obowiązują następujące relacje równoważności (jako konsekwencja tzw. granic niezwykłych):
Twierdzenie
Granica ilorazu (stosunku) dwóch nieskończenie małych wielkości nie ulegnie zmianie, jeśli jedną z nich (lub obie) zastąpimy wielkością równoważną.Twierdzenie to ma praktyczne znaczenie przy znajdowaniu granic (patrz przykład).
Przykład użycia
Wymiana SIN 2X wartość równoważna 2 X, otrzymujemySzkic historyczny
Pojęcie „nieskończenie małego” było omawiane już w starożytności w powiązaniu z koncepcją niepodzielnych atomów, ale nie było uwzględniane w matematyce klasycznej. Odrodziła się ponownie wraz z pojawieniem się w XVI wieku „metody niepodzielności” – podziału badanej figury na nieskończenie małe sekcje.
W XVII wieku miała miejsce algebraizacja rachunku nieskończenie małego. Zaczęto je definiować jako wielkości liczbowe, które są mniejsze od dowolnej ilości skończonej (niezerowej), a jednocześnie nie są równe zeru. Sztuka analizy polegała na sporządzeniu relacji zawierającej nieskończenie małe (różniczki) i następnie jej całkowaniu.
Matematycy ze starej szkoły wystawili tę koncepcję na próbę nieskończenie mały ostra krytyka. Michel Rolle napisał, że nowy rachunek różniczkowy jest „ zestaw genialnych błędów"; Voltaire zjadliwie zauważył, że rachunek różniczkowy to sztuka obliczania i dokładnego mierzenia rzeczy, których istnienia nie można udowodnić. Nawet Huygens przyznał, że nie rozumiał znaczenia różniczek wyższych rzędów.
Za ironię losu można uznać pojawienie się w połowie stulecia niestandardowych analiz, które dowiodły, że pierwotny punkt widzenia – rzeczywiste nieskończenie małe – również był spójny i mógł stanowić podstawę analiz.
Zobacz też
Fundacja Wikimedia. 2010.
Zobacz, co oznacza „nieskończona ilość” w innych słownikach:
NIESKOŃCZONA MAŁA ILOŚĆ- wielkość zmienna w pewnym procesie, jeżeli w tym procesie nieskończenie zbliża się (zmierza) do zera... Wielka encyklopedia politechniczna
Nieskończenie mały- ■ Coś nieznanego, ale związanego z homeopatią... Leksykon prawd powszechnych
NIESKOŃCZONE MAŁE FUNKCJE I ICH PODSTAWOWE WŁAŚCIWOŚCI
Funkcjonować y=f(x) zwany nieskończenie mały Na x → a albo kiedy X→∞, jeśli lub , tj. funkcja nieskończenie mała to funkcja, której granica w danym punkcie wynosi zero.
Przykłady.
Ustalmy następującą ważną zależność:
Twierdzenie. Jeśli funkcja y=f(x) reprezentowalny z x → a jako suma liczby stałej B i nieskończenie mała wielkość α(x): f (x)=b+ α(x) To .
I odwrotnie, jeśli , to fa (x)=b+α(x), Gdzie topór)– nieskończenie przy x → a.
Dowód.
Rozważmy podstawowe właściwości funkcji nieskończenie małych.
Twierdzenie 1. Suma algebraiczna dwóch, trzech i ogólnie dowolnej skończonej liczby nieskończenie małych jest funkcją nieskończenie małą.
Dowód. Przedstawmy dowód dla dwóch wyrazów. Pozwalać f(x)=α(x)+β(x), gdzie i . Musimy to udowodnić dla dowolnego dowolnego małego ε > Znaleziono 0 δ> 0, tak że dla X, spełniając nierówność |x – a|<δ , wykonane |f(x)|< ε.
Ustalmy więc dowolną liczbę ε > 0. Ponieważ zgodnie z warunkami twierdzenia α(x) jest funkcją nieskończenie małą, to istnieje takie δ 1 > 0, czyli |x – a|< δ1 mamy |α(x)|< ε / 2. Podobnie od β(x) jest nieskończenie małe, to istnieje takie δ 2 > 0, czyli |x – a|< δ2 mamy | β(x)|< ε / 2.
Weźmy δ=min(δ 1 , δ2 } .Następnie w sąsiedztwie punktu A promień δ każda z nierówności będzie spełniona |α(x)|< ε / 2 i | β(x)|< ε / 2. Dlatego w tej okolicy nie będzie
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
te. |f(x)|< ε, co należało udowodnić.
Twierdzenie 2. Iloczyn funkcji nieskończenie małej topór) dla ograniczonej funkcji k(x) Na x → a(albo kiedy x → ∞) jest funkcją nieskończenie małą.
Dowód. Ponieważ funkcja k(x) jest ograniczona, to jest liczba M tak, że dla wszystkich wartości X z jakiegoś sąsiedztwa punktu a|f(x)|≤M. Co więcej, od topór) jest nieskończenie małą funkcją w x → a, następnie dla dowolnego ε > 0 istnieje sąsiedztwo punktu A, w którym nierówność będzie zachowana |α(x)|< ε /M. Następnie w mniejszej z tych dzielnic, które mamy | αf|< ε /M= ε. A to oznacza, że af– nieskończenie małe. Z okazji x → ∞ dowód przeprowadza się analogicznie.
Z udowodnionego twierdzenia wynika:
Wniosek 1. Jeśli i wtedy.
Konsekwencja 2. Jeśli c= stała, następnie .
Twierdzenie 3. Stosunek funkcji nieskończenie małej α(x) na funkcję k(x), którego granica jest różna od zera, jest funkcją nieskończenie małą.
Dowód. Pozwalać ![]() . Następnie 1 /f(x) istnieje ograniczona funkcja. Dlatego ułamek
. Następnie 1 /f(x) istnieje ograniczona funkcja. Dlatego ułamek ![]() jest iloczynem funkcji nieskończenie małej i funkcji ograniczonej, tj. funkcja jest nieskończenie mała.
jest iloczynem funkcji nieskończenie małej i funkcji ograniczonej, tj. funkcja jest nieskończenie mała.
ZWIĄZEK MIĘDZY NIESKOŃCZONO MAŁYMI I NIESKOŃCZNIE DUŻYMI FUNKCJAMI
Twierdzenie 1. Jeśli funkcja k(x) jest nieskończenie duży w x → a, następnie funkcja 1 /f(x) jest nieskończenie małe przy x → a.
Dowód. Weźmy dowolną liczbę ε >0 i pokaż to niektórym δ>0 (w zależności od ε) dla wszystkich X, dla którego |x – a|<δ , nierówność jest spełniona, a to będzie oznaczać, że 1/f(x) jest funkcją nieskończenie małą. Rzeczywiście, od k(x) jest nieskończenie dużą funkcją w x → a, wtedy będzie δ>0 tak, że jak najszybciej |x – a|<δ , więc | f(x)|> 1/ ε. Ale potem o to samo X.
Przykłady.
Można także udowodnić twierdzenie odwrotne.
Twierdzenie 2. Jeśli funkcja k(x)- nieskończenie mały przy x → a(Lub x → ∞) i wtedy nie znika y= 1/f(x) jest nieskończenie dużą funkcją.
Przeprowadź dowód twierdzenia samodzielnie.
Przykłady.
Zatem najprostsze właściwości nieskończenie małych i nieskończenie dużych funkcji można zapisać za pomocą następujących relacji warunkowych: A≠ 0
TWIERDZENIA OGRANICZENIA
Twierdzenie 1. Granica sumy algebraicznej dwóch, trzech i ogólnie pewnej liczby funkcji jest równa sumie algebraicznej granic tych funkcji, tj.
Dowód. Dowód przeprowadzimy dla dwóch wyrazów, gdyż można to zrobić w ten sam sposób dla dowolnej liczby wyrazów. Pozwalać ![]() .Następnie f(x)=b+α(x) I g(x)=c+β(x), Gdzie α
I β
– funkcje nieskończenie małe. Stąd,
.Następnie f(x)=b+α(x) I g(x)=c+β(x), Gdzie α
I β
– funkcje nieskończenie małe. Stąd,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Ponieważ b+c jest stałą i α(x) + β(x) jest zatem funkcją nieskończenie małą
Przykład. .
Twierdzenie 2. Granica iloczynu dwóch, trzech i ogólnie skończonej liczby funkcji jest równa iloczynowi granic tych funkcji:
Dowód. Pozwalać ![]() . Stąd, f(x)=b+α(x) I g(x)=c+β(x) I
. Stąd, f(x)=b+α(x) I g(x)=c+β(x) I
fg = (b + α)(c + β) = bc + (bβ + cα + αβ).
Praca pne istnieje stała wartość. Funkcjonować bβ + do α + αβ w oparciu o właściwości nieskończenie małych funkcji istnieje nieskończenie mała ilość. Dlatego .
Wniosek 1. Stały współczynnik można przyjąć poza znak graniczny:
![]() .
.
Konsekwencja 2. Granica stopnia jest równa stopniowi granicznemu:
![]() .
.
Przykład.![]() .
.
Twierdzenie 3. Granica ilorazu dwóch funkcji jest równa ilorazowi granic tych funkcji, jeżeli granica mianownika jest różna od zera, tj.
 .
.
Dowód. Pozwalać . Stąd, f(x)=b+α(x) I g(x)=c+β(x), Gdzie α, β – nieskończenie małe. Rozważmy iloraz
Ułamek jest funkcją nieskończenie małą, ponieważ licznik jest funkcją nieskończenie małą, a mianownik ma granicę do 2 ≠0.
Przykłady.

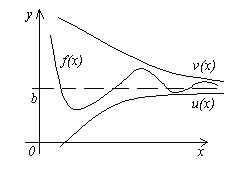
Twierdzenie 4. Niech będą dane trzy funkcje f(x), u(x) I v(x), spełniając nierówności u (x)≤f(x)≤ v(x). Jeśli funkcje ty(x) I v(x) mają ten sam limit w x → a(Lub x → ∞), a następnie funkcja k(x) zmierza do tej samej granicy, tj. Jeśli
![]() , To .
, To .
Znaczenie tego twierdzenia jest jasne z rysunku.
Dowód Twierdzenia 4 można znaleźć np. w podręczniku: Piskunov N. S. Rachunek różniczkowy i całkowy, tom 1 - M.: Nauka, 1985.
Twierdzenie 5. Jestem gruby x → a(Lub x → ∞) funkcja y=f(x) akceptuje wartości nieujemne y≥0 a jednocześnie dąży do granicy B, to granica ta nie może być ujemna: b≥0.
Dowód. Dowód przeprowadzimy przez sprzeczność. Udawajmy, że tak B<0 , Następnie |y – b|≥|b| i dlatego moduł różnicowy nie dąży do zera, gdy x → a. Ale wtedy y nie osiąga limitu B Na x → a, co jest sprzeczne z warunkami twierdzenia.
Twierdzenie 6. Jeśli dwie funkcje k(x) I g(x) dla wszystkich wartości argumentu X spełniają nierówność f(x) ≥ g(x) i mają granice, to nierówność jest spełniona b≥c.
Dowód. Zgodnie z warunkami twierdzenia f(x)-g(x) ≥0, zatem przez Twierdzenie 5 ![]() , Lub
, Lub ![]() .
.
GRANICE JEDNOSTRONNE

Do tej pory rozważaliśmy określenie granicy funkcji, gdy x → a w sposób dowolny, tj. granica funkcji nie zależała od sposobu jej umiejscowienia X w kierunku A, po lewej lub prawej stronie A. Jednak dość często spotyka się funkcje, które w tym warunku nie mają ograniczenia, ale mają granicę jeśli x → a, pozostając po jednej stronie A, w lewo lub w prawo (patrz rysunek). Dlatego wprowadzono pojęcia granic jednostronnych.
Jeśli k(x) zmierza do granicy B Na X zmierzający do określonej liczby A Więc X akceptuje tylko wartości mniejsze niż A, potem piszą i dzwonią blimit funkcji f(x) w punkcie a po lewej stronie.
Rachunek nieskończenie małych i dużych
Nieskończenie mały rachunek różniczkowy- obliczenia wykonywane na wielkościach nieskończenie małych, w których otrzymany wynik traktuje się jako nieskończoną sumę nieskończenie małych. Rachunek nieskończenie małych jest ogólną koncepcją rachunku różniczkowego i całkowego, która stanowi podstawę współczesnej matematyki wyższej. Pojęcie nieskończenie małej ilości jest ściśle powiązane z pojęciem granicy.
Nieskończenie mały
Podciąg A N zwany nieskończenie mały, Jeśli . Na przykład ciąg liczb jest nieskończenie mały.
Funkcja nazywa się nieskończenie małe w pobliżu punktu X 0 jeśli ![]() .
.
Funkcja nazywa się nieskończenie małe w nieskończoności, Jeśli ![]() Lub
Lub ![]() .
.
Nieskończenie mała jest także funkcja będąca różnicą między funkcją a jej granicą, to znaczy jeśli ![]() , To F(X) − A = α( X)
, .
, To F(X) − A = α( X)
, .
Nieskończenie duża ilość
Podciąg A N zwany nieskończenie duży, Jeśli ![]() .
.
Funkcja nazywa się nieskończenie duża w pobliżu punktu X 0 jeśli ![]() .
.
Funkcja nazywa się nieskończenie duży w nieskończoności, Jeśli ![]() Lub
Lub ![]() .
.
We wszystkich przypadkach zakłada się, że nieskończoność po prawej stronie równości ma określony znak (albo „plus”, albo „minus”). To jest na przykład funkcja X grzech X nie jest nieskończenie duży w .
Własności nieskończenie małe i nieskończenie duże
Porównanie wielkości nieskończenie małych
Jak porównać nieskończenie małe ilości?
Stosunek wielkości nieskończenie małych tworzy tzw. niepewność.
Definicje
Załóżmy, że mamy nieskończenie małe wartości α( X) i β( X) (lub, co nie jest istotne dla definicji, ciągi nieskończenie małe).
Aby obliczyć takie granice, wygodnie jest skorzystać z reguły L'Hopitala.
Przykłady porównawcze
Za pomocą O-symbolizm, uzyskane wyniki można zapisać w następującej formie X 5 = o(X 3). W tym przypadku prawdziwe są następujące wpisy: 2X 2 + 6X = O(X) I X = O(2X 2 + 6X).Równoważne wartości
Definicja
Jeśli , to nazywa się nieskończenie małe wielkości α i β równowartość ().
Jest oczywiste, że ilości równoważne są szczególnym przypadkiem nieskończenie małych ilości tego samego rzędu małości.
Gdy obowiązują następujące relacje równoważności: , , ![]() .
.
Twierdzenie
Granica ilorazu (stosunku) dwóch nieskończenie małych wielkości nie ulegnie zmianie, jeśli jedną z nich (lub obie) zastąpimy wielkością równoważną.Twierdzenie to ma praktyczne znaczenie przy znajdowaniu granic (patrz przykład).
Przykład użycia
Wymiana SIN 2X wartość równoważna 2 X, otrzymujemySzkic historyczny
Pojęcie „nieskończenie małego” było omawiane już w starożytności w powiązaniu z koncepcją niepodzielnych atomów, ale nie było uwzględniane w matematyce klasycznej. Odrodziła się ponownie wraz z pojawieniem się w XVI wieku „metody niepodzielności” – podziału badanej figury na nieskończenie małe sekcje.
W XVII wieku miała miejsce algebraizacja rachunku nieskończenie małego. Zaczęto je definiować jako wielkości liczbowe, które są mniejsze od dowolnej ilości skończonej (niezerowej), a jednocześnie nie są równe zeru. Sztuka analizy polegała na sporządzeniu relacji zawierającej nieskończenie małe (różniczki) i następnie jej całkowaniu.
Matematycy ze starej szkoły wystawili tę koncepcję na próbę nieskończenie mały ostra krytyka. Michel Rolle napisał, że nowy rachunek różniczkowy jest „ zestaw genialnych błędów"; Voltaire zjadliwie zauważył, że rachunek różniczkowy to sztuka obliczania i dokładnego mierzenia rzeczy, których istnienia nie można udowodnić. Nawet Huygens przyznał, że nie rozumiał znaczenia różniczek wyższych rzędów.
Spory w Paryskiej Akademii Nauk dotyczące zasadności analizy stały się na tyle skandaliczne, że Akademia pewnego razu całkowicie zabroniła swoim członkom wypowiadać się na ten temat (dotyczyło to głównie Rolle'a i Varignona). W 1706 roku Rolle publicznie wycofał swoje zastrzeżenia, ale dyskusje trwały nadal.
W 1734 roku słynny angielski filozof, biskup George Berkeley, opublikował sensacyjną broszurę, znaną pod skróconym tytułem „ Analityk" Jego pełna nazwa: „ Analityk lub dyskurs skierowany do niewierzącego matematyka, w którym zadaje się pytanie, czy przedmiot, zasady i wnioski współczesnej analizy są jaśniej postrzegane lub jaśniej wywnioskowane niż religijne sakramenty i artykuły wiary».
Analityk zawierał dowcipną i w dużej mierze uczciwą krytykę rachunku nieskończenie małego. Berkeley uznał metodę analizy za niezgodną z logiką i napisał, że: „ niezależnie od tego, jak przydatne może być, można je uznać jedynie za rodzaj przypuszczenia; zręczna umiejętność, sztuka, a raczej podstęp, ale nie jako metoda dowodu naukowego" Cytując sformułowanie Newtona o przyroście wielkości bieżących „na samym początku ich powstawania lub zanikania”, Berkeley ironicznie: „ nie są to ani ilości skończone, ani nieskończenie małe, ani nawet nic. Czy nie moglibyśmy nazwać ich duchami zmarłych wielkości?... I jak w ogóle możemy mówić o związku między rzeczami, które nie mają wielkości?.. Każdy, kto potrafi przetrawić drugą lub trzecią fluktuację [pochodną], drugą lub trzecią różnicy, nie powinien, ponieważ wydaje mi się, że doszukuję się błędu w czymś w teologii».
Niemożliwe jest, pisze Berkeley, wyobrażenie sobie prędkości chwilowej, to znaczy prędkości w danej chwili i w danym punkcie, ponieważ pojęcie ruchu obejmuje pojęcia (skończonej niezerowej) przestrzeni i czasu.
W jaki sposób analiza daje prawidłowe wyniki? Berkeley doszedł do wniosku, że można to wytłumaczyć obecnością kilku błędów we wnioskach analitycznych i zilustrował to przykładem paraboli. Ciekawe, że niektórzy główni matematycy (na przykład Lagrange) zgodzili się z nim.
Do paradoksalnej sytuacji doszło, gdy rygorystyczność i płodność w matematyce kolidowały ze sobą. Pomimo zastosowania nielegalnych działań ze słabo zdefiniowanymi koncepcjami, liczba bezpośrednich błędów była zaskakująco mała – z pomocą przyszła intuicja. A jednak przez cały XVIII wiek analiza matematyczna rozwijała się szybko, w zasadzie bez żadnego uzasadnienia. Jego skuteczność była niesamowita i mówiła sama za siebie, jednak znaczenie różnicy nadal było niejasne. Szczególnie często mylony był nieskończenie mały przyrost funkcji z jej częścią liniową.
Przez cały XVIII wiek podejmowano ogromne wysiłki, aby naprawić sytuację, a brali w nich udział najlepsi matematycy stulecia, ale dopiero Cauchy'emu udało się przekonująco zbudować podstawy analizy na początku XIX wieku. Ściśle zdefiniował podstawowe pojęcia - granicę, zbieżność, ciągłość, różniczkę itp., po czym rzeczywiste nieskończenie małe zniknęły z nauki. Niektóre pozostałe subtelności wyjaśniono później
Twierdzenie 2.4. Jeśli ciągi (x n) i (y n) są zbieżne i x n ≤ y n, n > n 0, to lim x n ≤ lim y n.
Niech lim xn = a, |
lim yn = b i a > b. Z definicji 2,4 limitów |
||||||||||||||||||||
sekwencje według numeru ε = |
istnieje liczba N taka, że |
||||||||||||||||||||
Dlatego n > max(n0 , N) yn< |
< xn , что противоречит |
||||||||||||||||||||
stan : schorzenie. |
|||||||||||||||||||||
Komentarz. Jeśli ciągi (xn), (yn) są zbieżne dla |
|||||||||||||||||||||
wszystkie n > n0 |
xn< yn , то можно утверждать лишь, что lim xn |
≤ lim yn . |
|||||||||||||||||||
Aby to zobaczyć, wystarczy rozważyć sekwencje
i yn = |
||||
Poniższe wyniki wynikają bezpośrednio z Definicji 2.4.
Twierdzenie 2.5. Jeśli ciąg liczb (x n) jest zbieżny i lim x n< b (b R), то N N: x n < b, n >N.
Konsekwencja. Jeżeli ciąg (xn) jest zbieżny i lim xn 6= 0, to
N N: sgn xn = sgn(lim xn), n > N.
Twierdzenie 2.6. Niech ciągi (x n), (y n), (z n) spełniają warunki:
1) x n ≤ yn ≤ zn, n > n0,
2) sekwencje(x n) i (z n) zbiegają się i lim x n = lim z n = a.
Wtedy ciąg (y n ) jest zbieżny i lim y n = a.
2.1.3 Nieskończenie małe sekwencje
Definicja 2.7. Ciąg liczb (x n) nazywany jest nieskończenie małym (nieskończenie małym), jeśli jest zbieżny i lim x n = 0.
Zgodnie z definicją 2.4 granicy ciągu liczbowego, definicja 2.7 jest równoważna następującemu:
Definicja 2.8. Ciąg liczb (x n) nazywamy nieskończenie małym, jeśli dla dowolnej liczby dodatniej ε istnieje taka liczba N = N(ε), że dla wszystkich n > N elementy x n tego ciągu spełniają nierówność |x n |< ε.
Zatem (xn) - b.m. ε > 0 N = N(ε) : n > N |xn |< ε.
Z przykładów 2, 3 i uwagi 1 do twierdzenia 2.3 otrzymujemy to później
ważność ( |
q-n |
są nieskończone |
||||||||||||
Własności ciągów nieskończenie małych opisują następujące twierdzenia.
Twierdzenie 2.7. Suma skończonej liczby nieskończenie małych ciągów jest ciągiem nieskończenie małym.
Niech ciągi (xn), (yn) będą nieskończenie małe. Pokażmy, że (xn + yn) również będzie jednością. Ustawmy ε > 0. Wtedy mamy liczbę
N1 = N1 (ε) tak, że |
||||
|xn |< |
N>N1, |
|||
i istnieje liczba N2 = N2 (ε) taka, że |
||||
|yn |< |
N>N2. |
|||
Oznaczmy przez N = max(N1, N2). Dla n > N obowiązują nierówności (2.1) i (2.2). Zatem dla n > N
|xn + yn | ≤ |xn | + |yn |< 2 + 2 = ε.
Oznacza to, że ciąg (xn +yn) jest nieskończenie mały. Twierdzenie o sumie skończonej liczby ciągów nieskończenie małych
Wynika to z tego, co zostało udowodnione przez indukcję.
Twierdzenie 2.8. Iloczyn ciągu nieskończenie małego i ciągu ograniczonego jest nieskończenie mały.
Niech (xn) będzie ciągiem ograniczonym, a (yn) nieskończenie małym ciągiem. Zgodnie z definicją 2.6 ciągu ograniczonego istnieje liczba M > 0 taka, że
|xn | ≤ M, n N. |
Ustalmy dowolną liczbę ε > 0. Ponieważ (yn) jest ciągiem nieskończenie małym, istnieje liczba N = N(ε) taka, że
Dlatego sekwencja (xn yn ) jest nieskończenie małe.

Wniosek 1. Iloczyn ciągu nieskończenie małego i ciągu zbieżnego jest ciągiem nieskończenie małym.
Wniosek 2. Iloczyn dwóch nieskończenie małych ciągów jest ciągiem nieskończenie małym.
Używając nieskończenie małych sekwencji, definicję sekwencji zbieżnej można spojrzeć inaczej.
Lemat 2.1. Aby liczba a była granicą ciągu liczbowego (x n), konieczne i wystarczające jest istnienie reprezentacji x n = a + α n, n N, w której (α n) jest ciągiem nieskończenie małym.
Konieczność. Niech lim xn = a i a R. Następnie
ε > 0 N = N(ε) N: n > N |xn – a|< ε.
Jeżeli ustalimy αn = xn − a, n N, to otrzymamy, że (αn) jest ciągiem nieskończenie małym oraz xn = a + αn, n N.
Adekwatność. Niech ciąg (xn) będzie taki, że istnieje liczba a, dla której xn = a + αn, n N i lim αn = 0. Ustalmy dowolną liczbę dodatnią ε. Ponieważ lim αn = 0, to istnieje liczba N = N(ε) N taka, że |αn |< ε, n >N. Oznacza to, że w innych zapisach n > N |xn − a|< ε. Это означает, что lim xn = a.
Zastosujmy Lemat 2.1 do ważnego konkretnego przykładu.
Lemat 2.2. lim n n = 1.
√ √
Ponieważ dla wszystkich n > 1 n n > 1, wówczas n n = 1 + αn i αn > 0 dla
wszystkie n > 1. Dlatego n = (1 + α |
)n = 1 + nα |
+ αn. |
|||||||||||||||
Ponieważ wszystkie terminy są dodatnie, n |
|||||||||||||||||
Niech ε > 0. Ponieważ |
2/n< ε для всех n >2/ε , zatem zakładając |
||||||||||||||||
N = max(1, ), otrzymujemy 0< αn < ε, n >N. Dlatego
ciąg (αn) jest nieskończenie mały i zgodnie z lematem
2,1, lim n n = 1. √
Konsekwencja. Jeśli a > 1, to lim n a = 1,√ √
Twierdzenie wynika z nierówności 1< n a ≤ n n , n >[A].
2.1.4 Działania arytmetyczne na ciągach
Korzystając z Lematu 2.1 i własności ciągów nieskończenie małych, łatwo jest otrzymać twierdzenia o granicach ciągów otrzymanych za pomocą działań arytmetycznych na ciągach zbieżnych.

|b| 3|b|
2 < |y n | < 2
Twierdzenie 2.9. Niech ciągi liczbowe (x n) i (y n) są zbieżne. Wtedy obowiązują następujące stwierdzenia:
1) ciąg (x n ± y n ) jest zbieżny i
lim(xn ± yn) = lim xn ± lim yn;
2) ciąg (x n · y n ) jest zbieżny i
lim(xn · yn) = lim xn · lim yn;
3) jeśli lim y n 6= 0, to stosunek x n /y n definiuje się rozpoczynając od
pewna liczba, ciąg ( x n ) jest zbieżny i
Zgodnie z Twierdzeniem 2.8 i wnioskiem 1, ciągi (a · βn), (b · αn), (αn · βn) są nieskończenie małe. Zgodnie z Twierdzeniem 2.7 ciąg (aβn + bαn + αn βn) jest nieskończenie mały. Twierdzenie 2) wynika z przedstawienia (2.5) lematu 2.1.
Przejdźmy do stwierdzenia 3). Warunek: lim yn = b 6= 0. Na mocy Twierdzenia 2.3. ciąg (|yn |) jest zbieżny i lim |yn | = |b| 6= 0. Zatem mając daną liczbę ε = |b|/2, istnieje liczba N taka, że n > N
0 < | 2 b| = |b| −
Dlatego yn =6 0 i 3|b|< y n < |b| , n >N.
Zatem iloraz xn /yn jest zdefiniowany dla wszystkich n > N, a sekwencja (1/yn) jest ograniczona. Rozważ różnicę dla wszystkich n > N
(αn b - aβn). |
|||||||||||||||||||||
Podciąg |
αn b |
aβn |
Nieskończenie mały |
||||||||||||||||||
ograniczony. Zgodnie z twierdzeniem 2.8 sekwencja |
|||||||||||||||||||||
- b |
|||||||||||||||||||||
bardzo mały. Zatem poprzez Lemat 2.1, twierdzenie 3) jest udowodnione. Wniosek 1. Jeśli ciąg (xn) jest zbieżny, to dla dowolnego
Dla dowolnej liczby c ciąg (c · xn) jest zbieżny i lim(cxn) = c · lim xn.
Funkcje nieskończenie małe
Wywoływana jest funkcja %%f(x)%%. nieskończenie mały(b.m.) z %%x \to a \in \overline(\mathbb(R))%%, jeśli przy tej tendencji argumentu granica funkcji jest równa zeru.
Koncepcja b.m. Funkcja jest nierozerwalnie powiązana z instrukcjami zmiany jej argumentu. Możemy porozmawiać o b.m. działa przy %%a \to a + 0%% i %%a \to a - 0%%. Zwykle b.m. funkcje są oznaczone pierwszymi literami alfabetu greckiego %%\alpha, \beta, \gamma, \ldots%%
Przykłady
- Funkcja %%f(x) = x%% to b.m. przy %%x \to 0%%, ponieważ jego granica w punkcie %%a = 0%% wynosi zero. Zgodnie z twierdzeniem o związku granicy dwustronnej z granicą jednostronną funkcja ta ma postać b.m. zarówno z %%x \to +0%%, jak i %%x \to -0%%.
- Funkcja %%f(x) = 1/(x^2)%% - b.m. przy %%x \to \infty%% (jak również przy %%x \to +\infty%% i %%x \to -\infty%%).
Niezerowa liczba stała, niezależnie od tego, jak mała jest jej wartość bezwzględna, nie jest b.m. funkcjonować. W przypadku liczb stałych jedynym wyjątkiem jest zero, ponieważ funkcja %%f(x) \equiv 0%% ma granicę zera.
Twierdzenie
Funkcja %%f(x)%% ma w punkcie %%a \in \overline(\mathbb(R))%% rozszerzonej osi liczbowej końcową granicę równą liczbie %%b%% wtedy i tylko jeśli ta funkcja jest równa sumie tej liczby %%b%% i b.m. funkcje %%\alpha(x)%% z %%x \to a%% lub $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Leftrightarrow \left(f(x) = b + \alpha(x)\right) \land \left(\lim\limits_(x \to a)(\alpha(x) = 0)\right). $$
Własności funkcji nieskończenie małych
Zgodnie z regułami przejścia do granicy z %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, następują następujące stwierdzenia:
- Suma końcowej liczby b.m. funkcje dla %%x \to a%% to b.m. w %%x \do a%%.
- Iloczyn dowolnej liczby b.m. funkcje dla %%x \to a%% to b.m. w %%x \do a%%.
Produkt b.m. funkcji w %%x \to a%% i funkcją ograniczoną w pewnym przebitym sąsiedztwie %%\stackrel(\circ)(\text(U))(a)%% punktu a, jest b.m. w %%x \do funkcji%%.
Jasne jest, że iloczyn funkcji stałej i b.m. w %%x \to a%% jest b.m. funkcja w %%x \to a%%.
Równoważne funkcje nieskończenie małe
Wywoływane są nieskończenie małe funkcje %%\alpha(x), \beta(x)%% dla %%x \to a%% równowartość i napisz %%\alpha(x) \sim \beta(x)%%, if
$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x) )(\alfa(x))) = 1. $$
Twierdzenie o podstawieniu b.m. funkcje równoważne
Niech %%\alpha(x), \alpha_1(x), \beta(x), \beta_1(x)%% będzie b.m. funkcje dla %%x \to a%%, gdzie %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, następnie $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ limity_(x \do a)(\frac(\alpha_1(x))(\beta_1(x))). $$
Odpowiednik b.m. Funkcje.
Niech %%\alpha(x)%% będzie b.m. wówczas funkcja w %%x \to a%%.
- %%\sin(\alfa(x)) \sim \alfa(x)%%
- %%\displaystyle 1 - \cos(\alfa (x)) \sim \frac(\alfa ^2(x))(2)%%
- %%\tan \alfa(x) \sim \alfa(x)%%
- %%\arcsin\alfa(x) \sim \alfa(x)%%
- %%\arctan\alfa(x) \sim \alfa(x)%%
- %%\ln(1 + \alfa(x)) \sim \alfa(x)%%
- %%\displaystyle\sqrt[n](1 + \alfa(x)) - 1 \sim \frac(\alfa(x))(n)%%
- %%\displaystyle a^(\alfa(x)) - 1 \sim \alfa(x) \ln(a)%%
Przykład
$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(tablica) $$
Nieskończenie duże funkcje
Wywoływana jest funkcja %%f(x)%%. nieskończenie duży(b.b.) z %%x \to a \in \overline(\mathbb(R))%%, jeśli przy tej tendencji argumentu funkcja ma nieskończoną granicę.
Podobny do b.m. koncepcja funkcji b.b. Funkcja jest nierozerwalnie powiązana z instrukcjami zmiany jej argumentu. Możemy porozmawiać o b.b. działa z %%x \to a + 0%% i %%x \to a - 0%%. Określenie „nieskończenie duża” nie mówi o wartości bezwzględnej funkcji, ale o charakterze jej zmiany w pobliżu rozpatrywanego punktu. Żadna stała liczba, niezależnie od tego, jak duża jest jej wartość bezwzględna, nie jest nieskończenie duża.
Przykłady
- Funkcja %%f(x) = 1/x%% - b.b. przy %%x \do 0%%.
- Funkcja %%f(x) = x%% - b.b. w %%x \to \infty%%.
Jeżeli warunki definicji $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(tablica) $$
potem o tym rozmawiają pozytywny Lub negatywny nocleg ze śniadaniem. przy funkcji %%a%%.
Przykład
Funkcja %%1/(x^2)%% - dodatni t.b. przy %%x \do 0%%.
Związek pomiędzy b.b. i b.m. Funkcje
Jeśli %%f(x)%% to b.b. z funkcją %%x \to a%%, następnie %%1/f(x)%% - b.m.
w %%x \do a%%. Jeśli %%\alpha(x)%% - b.m. dla %%x \to a%% jest niezerową funkcją w pewnym przebitym sąsiedztwie punktu %%a%%, wówczas %%1/\alpha(x)%% jest b.b. w %%x \do a%%.
Własności nieskończenie dużych funkcji
Przedstawmy kilka właściwości bb. Funkcje. Właściwości te wynikają bezpośrednio z definicji b.b. funkcje i własności funkcji mających skończone granice, a także z twierdzenia o związku pomiędzy b.b. i b.m. Funkcje.
- Iloczyn skończonej liczby b.b. funkcje dla %%x \to a%% to b.b. funkcja w %%x \to a%%. Rzeczywiście, jeśli %%f_k(x), k = \overline(1, n)%% - b.b. funkcjonuje w %%x \to a%%, następnie w pewnym przebitym sąsiedztwie punktu %%a%% %%f_k(x) \ne 0%%, oraz na podstawie twierdzenia o połączeniu b.b. i b.m. funkcje %%1/f_k(x)%% - b.m. funkcja w %%x \to a%%. Okazuje się, że %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m funkcja dla %%x \to a%% i %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funkcja w %%x \to a%%.
- Produkt b.b. funkcje dla %%x \to a%%, a funkcja, która w pewnym przebitym sąsiedztwie punktu %%a%% w wartości bezwzględnej jest większa od stałej dodatniej, to b.b. funkcja w %%x \to a%%. W szczególności produkt b.b. funkcja z %%x \to a%% i funkcja, która ma skończoną niezerową granicę w punkcie %%a%% będzie b.b. funkcja w %%x \to a%%.
Suma dwóch b.b. działa w %%x \to a%% występuje niepewność. W zależności od znaku wyrazów charakter zmiany takiej sumy może być bardzo różny.
Przykład
Niech zostaną podane funkcje %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. działa w %%x \to \infty%%. Następnie:
- %%f(x) + g(x) = 3x%% - b.b. funkcja w %%x \to \infty%%;
- %%f(x) + h(x) = 0%% - b.m. funkcja w %%x \to \infty%%;
- %%h(x) + v(x) = \sin x%% nie ma ograniczenia w %%x \to \infty%%.
Suma funkcji ograniczonej w pewnym przebitym sąsiedztwie punktu %%a%% i b.b. funkcje z %%x \to a%% to b.b. funkcja w %%x \to a%%.
Na przykład funkcje %%x - \sin x%% i %%x + \cos x%% to b.b. w %%x \to \infty%%.
