Sekuenca pafundësisht të vogla - përkufizimi dhe vetitë. Shembuj Çfarë sasie quhet infinitimale
Llogaritja e infinitezimaleve dhe të mëdhave
Njehsimi infinitimal- llogaritjet e kryera me madhësi infiniteminale, në të cilat rezultati i prejardhur konsiderohet si një shumë e pafundme infinitezimalesh. Llogaritja e infinitezimaleve është një koncept i përgjithshëm për llogaritjet diferenciale dhe integrale, i cili përbën bazën e matematikës së lartë moderne. Koncepti i një sasie infiniteminale është i lidhur ngushtë me konceptin e kufirit.
Pafundësisht i vogël
Pasoja a n thirrur pafundësisht i vogël, Nëse . Për shembull, një sekuencë numrash është pafundësisht e vogël.
Funksioni thirret pafundësisht i vogël në afërsi të një pike x 0 nëse ![]() .
.
Funksioni thirret pafundësisht i vogël në pafundësi, Nëse ![]() ose
ose ![]() .
.
Gjithashtu infinitezimal është një funksion që është ndryshimi midis një funksioni dhe kufirit të tij, domethënë nëse ![]() , Kjo f(x) − a = α( x)
, .
, Kjo f(x) − a = α( x)
, .
Sasi pafundësisht e madhe
Në të gjitha formulat e mëposhtme, pafundësia në të djathtë të barazisë nënkuptohet të ketë një shenjë të caktuar (ose "plus" ose "minus"). Ky është, për shembull, funksioni x mëkat x, i pakufizuar nga të dyja anët, nuk është pafundësisht i madh në .
Pasoja a n thirrur pafundësisht i madh, Nëse ![]() .
.
Funksioni thirret pafundësisht i madh në afërsi të një pike x 0 nëse ![]() .
.
Funksioni thirret pafundësisht i madh në pafundësi, Nëse ![]() ose
ose ![]() .
.
Vetitë e pafundësisht të vogla dhe pafundësisht të mëdha
Krahasimi i madhësive infiniteminale
Si të krahasoni sasitë infinite të vogla?
Raporti i sasive infiniteminale formon të ashtuquajturën pasiguri.
Përkufizimet
Supozoni se kemi vlera infiniteminale α( x) dhe β( x) (ose, që nuk është e rëndësishme për përkufizimin, sekuenca pafundësisht të vogla).
Për të llogaritur kufij të tillë është e përshtatshme të përdoret rregulli i L'Hopital.
Shembuj krahasues
Duke përdorur RRETH-simbolizmi, rezultatet e fituara mund të shkruhen në formën e mëposhtme x 5 = o(x 3). Në këtë rast, shënimet e mëposhtme janë të vërteta: 2x 2 + 6x = O(x) Dhe x = O(2x 2 + 6x).Vlerat ekuivalente
Përkufizimi
Nëse , atëherë quhen madhësitë infiniteminale α dhe β ekuivalente ().
Është e qartë se sasitë ekuivalente janë një rast i veçantë i sasive infiniteminale të rendit të njëjtë të vogëlsisë.
Kur relacionet e mëposhtme të ekuivalencës janë të vlefshme (si pasojë e të ashtuquajturave kufij të shquar):
Teorema
Kufiri i herësit (raportit) të dy sasive infiniteminale nuk do të ndryshojë nëse njëra prej tyre (ose të dyja) zëvendësohet nga një sasi ekuivalente..Kjo teoremë ka rëndësi praktike gjatë gjetjes së kufijve (shih shembullin).
Shembull përdorimi
Duke zëvendësuar sin 2x vlerë ekuivalente 2 x, marrimSkicë historike
Koncepti i "pafundësishëm" u diskutua në kohët e lashta në lidhje me konceptin e atomeve të pandarë, por nuk u përfshi në matematikën klasike. Ajo u ringjall përsëri me ardhjen e "metodës së të pandarëve" në shekullin e 16-të - duke e ndarë figurën në studim në seksione pafundësisht të vogla.
Në shekullin e 17-të, u bë algjebrizimi i llogaritjes infinitimale. Ato filluan të përkufizohen si madhësi numerike që janë më të vogla se çdo sasi e fundme (jo zero) dhe megjithatë nuk janë të barabarta me zero. Arti i analizës konsistonte në hartimin e një relacioni që përmban infinitezimale (diferenciale) dhe më pas integrimin e tij.
Matematikanët e shkollës së vjetër e vënë në provë konceptin pafundësisht i vogël kritika të ashpra. Michel Rolle shkroi se llogaritja e re është " grup gabimesh gjeniale"; Volteri vërejti në mënyrë kaustike se llogaritja është arti i llogaritjes dhe matjes së saktë të gjërave, ekzistenca e të cilave nuk mund të vërtetohet. Edhe Huygens pranoi se ai nuk e kuptonte kuptimin e diferencialeve të rendit më të lartë.
Si një ironi e fatit, mund të konsiderohet shfaqja në mesin e shekullit të analizave jo standarde, e cila vërtetoi se këndvështrimi origjinal - infinitezimalet aktuale - ishte gjithashtu konsistent dhe mund të përdorej si bazë për analizë.
Shiko gjithashtu
Fondacioni Wikimedia. 2010.
Shihni se çfarë është "sasia pafundësisht e vogël" në fjalorë të tjerë:
SASSI PA FUNDI I VOGËL- një sasi e ndryshueshme në një proces të caktuar, nëse në këtë proces pafundësisht i afrohet (priret) zeros... Enciklopedia e Madhe Politeknike
Pafundësisht i vogël- ■ Diçka e panjohur, por e lidhur me homeopatinë... Leksiku i të vërtetave të përbashkëta
FUNKSIONET E PAFINIT TË VOGLA DHE VETITË THEMELORE TË TYRE
Funksioni y=f(x) thirrur pafundësisht i vogël në x→a ose kur x→∞, nëse ose , d.m.th. një funksion pafundësisht i vogël është një funksion kufiri i të cilit në një pikë të caktuar është zero.
Shembuj.
Le të vendosim marrëdhënien e mëposhtme të rëndësishme:
Teorema. Nëse funksioni y=f(x) e perfaqesueshme me x→a si shumë e një numri konstant b dhe magnitudë pafundësisht të vogël α(x): f (x)=b+ α(x) Se .
Në të kundërt, nëse , atëherë f (x)=b+α(x), Ku a(x)– pafundësisht i vogël në x→a.
Dëshmi.
Le të shqyrtojmë vetitë themelore të funksioneve infiniteminale.
Teorema 1. Shuma algjebrike e dy, tre, dhe në përgjithësi çdo numër i kufizuar i infinitezimaleve është një funksion infinitesimal.
Dëshmi. Le të japim një provë për dy terma. Le f(x)=α(x)+β(x), ku dhe . Duhet të vërtetojmë se për çdo ε të vogël arbitrare > 0 u gjet δ> 0, e tillë që për x, duke kënaqur pabarazinë |x – a|<δ , kryer |f(x)|< ε.
Pra, le të rregullojmë një numër arbitrar ε > 0. Meqenëse sipas kushteve të teoremës α(x)është një funksion pafundësisht i vogël, atëherë ekziston δ 1 i tillë > 0, që është |x – a|< δ 1 kemi |α(x)|< ε / 2. Po kështu, që nga β(x)është pafundësisht i vogël, atëherë ekziston δ 2 > 0, që është |x – a|< δ 2 kemi | β(x)|< ε / 2.
Le ta marrim δ=min(δ 1 , δ2 } .Pastaj në lagjen e pikës a rreze δ secila nga pabarazitë do të plotësohet |α(x)|< ε / 2 dhe | β(x)|< ε / 2. Prandaj, në këtë lagje do të ketë
|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)|< ε /2 + ε /2= ε,
ato. |f(x)|< ε, që është ajo që duhej vërtetuar.
Teorema 2. Produkt i një funksioni pafundësisht të vogël a(x) për një funksion të kufizuar f(x) në x→a(ose kur x→∞) është një funksion pafundësisht i vogël.
Dëshmi. Që nga funksioni f(x)është i kufizuar, atëherë ka një numër M të tillë që për të gjitha vlerat x nga ndonjë lagje e një pike a|f(x)|≤M. Për më tepër, që nga a(x)është një funksion pafundësisht i vogël në x→a, pastaj për një ε arbitrare > 0 ka një lagje të pikës a, në të cilën do të mbahet pabarazia |α(x)|< ε /M. Pastaj në më të vogël nga këto lagje kemi | αf|< ε /M= ε. Dhe kjo do të thotë se af– pafundësisht i vogël. Për rastin x→∞ vërtetimi kryhet në mënyrë të ngjashme.
Nga teorema e provuar rezulton:
Përfundimi 1. Nëse dhe, atëherë.
Përfundimi 2. Nëse c= konst, atëherë .
Teorema 3. Raporti i një funksioni pafundësisht të vogël α(x) për funksion f(x), kufiri i të cilit është i ndryshëm nga zero, është një funksion pafundësisht i vogël.
Dëshmi. Le ![]() . Pastaj 1 /f(x) ka një funksion të kufizuar. Prandaj thyesa
. Pastaj 1 /f(x) ka një funksion të kufizuar. Prandaj thyesa ![]() është prodhim i një funksioni infinitimal dhe i një funksioni të kufizuar, d.m.th. funksioni është infinit i vogël.
është prodhim i një funksioni infinitimal dhe i një funksioni të kufizuar, d.m.th. funksioni është infinit i vogël.
MARRËDHËNIET MIDIS FUNKSIONET PA FINFIFITË TË VOGLA DHE PA FINFIFITË TË MËDHA
Teorema 1. Nëse funksioni f(x)është pafundësisht i madh në x→a, pastaj funksioni 1 /f(x)është pafundësisht i vogël në x→a.
Dëshmi. Le të marrim një numër arbitrar ε >0 dhe tregojeni këtë për disa δ>0 (në varësi të ε) për të gjithë x, per cilin |x – a|<δ , pabarazia plotësohet dhe kjo do të thotë se 1/f(x)është një funksion pafundësisht i vogël. Në të vërtetë, që nga f(x)është një funksion pafundësisht i madh në x→a, atëherë do të ketë δ>0 të tillë që sapo |x – a|<δ , pra | f(x)|> 1/ ε. Por pastaj për të njëjtën gjë x.
Shembuj.
Mund të vërtetohet edhe teorema e kundërt.
Teorema 2. Nëse funksioni f(x)- pafundësisht i vogël në x→a(ose x→∞) dhe nuk zhduket, atëherë y= 1/f(x)është një funksion pafundësisht i madh.
Kryeni vetë vërtetimin e teoremës.
Shembuj.
Kështu, vetitë më të thjeshta të funksioneve infinitimale dhe pafundësisht të mëdha mund të shkruhen duke përdorur marrëdhëniet e mëposhtme të kushtëzuara: A≠ 0
TEOREMA KUFIZORE
Teorema 1. Kufiri i shumës algjebrike të dy, tre dhe përgjithësisht një numër i caktuar funksionesh është i barabartë me shumën algjebrike të kufijve të këtyre funksioneve, d.m.th.
Dëshmi. Le ta kryejmë vërtetimin për dy terma, pasi mund të bëhet në të njëjtën mënyrë për çdo numër termash. Le ![]() .Pastaj f(x)=b+α(x) Dhe g(x)=c+β(x), Ku α
Dhe β
– funksione infiniteminale. Prandaj,
.Pastaj f(x)=b+α(x) Dhe g(x)=c+β(x), Ku α
Dhe β
– funksione infiniteminale. Prandaj,
f(x) + g(x)=(b + c) + (α(x) + β(x)).
Sepse b+cështë një konstante dhe α(x) + β(x)është një funksion pafundësisht i vogël, pra
Shembull. .
Teorema 2. Kufiri i prodhimit të dy, tre dhe përgjithësisht një numri të kufizuar funksionesh është i barabartë me produktin e kufijve të këtyre funksioneve:
Dëshmi. Le ![]() . Prandaj, f(x)=b+α(x) Dhe g(x)=c+β(x) Dhe
. Prandaj, f(x)=b+α(x) Dhe g(x)=c+β(x) Dhe
fg = (b + α) (c + β) = bc + (bβ + cα + αβ).
Puna para Krishtit ka një vlerë konstante. Funksioni bβ + c α + αβ në bazë të vetive të funksioneve infinitimale, ekziston një sasi infinite vogël. Kjo është arsyeja pse.
Përfundimi 1. Faktori konstant mund të merret përtej shenjës kufitare:
![]() .
.
Përfundimi 2. Kufiri i shkallës është i barabartë me shkallën kufi:
![]() .
.
Shembull.![]() .
.
Teorema 3. Kufiri i herësit të dy funksioneve është i barabartë me herësin e kufijve të këtyre funksioneve nëse kufiri i emëruesit është i ndryshëm nga zero, d.m.th.
 .
.
Dëshmi. Le . Prandaj, f(x)=b+α(x) Dhe g(x)=c+β(x), Ku α, β – pafundësisht i vogël. Le të shqyrtojmë herësin
Një thyesë është një funksion pafundësisht i vogël sepse numëruesi është një funksion pafundësisht i vogël dhe emëruesi ka një kufi c 2 ≠0.
Shembuj.

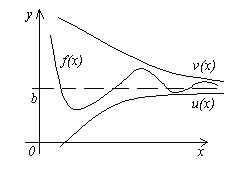
Teorema 4. Le të jepen tre funksione f(x), u(x) Dhe v(x), duke kënaqur pabarazitë u (x)≤f(x)≤ v(x). Nëse funksionet u(x) Dhe v(x) kanë të njëjtin limit në x→a(ose x→∞), pastaj funksioni f(x) priret në të njëjtin kufi, d.m.th. Nëse
![]() , Kjo .
, Kjo .
Kuptimi i kësaj teoreme është i qartë nga figura.
Vërtetimi i Teoremës 4 mund të gjendet, për shembull, në librin shkollor: Piskunov N. S. Llogaritja diferenciale dhe integrale, vëll 1 - M.: Nauka, 1985.
Teorema 5. Nëse në x→a(ose x→∞) funksion y=f(x) pranon vlera jo negative y≥0 dhe në të njëjtën kohë tenton në kufi b, atëherë ky kufi nuk mund të jetë negativ: b≥0.
Dëshmi. Ne do ta kryejmë vërtetimin me kontradiktë. Le të pretendojmë se b<0 , Pastaj |y – b|≥|b| dhe, për rrjedhojë, moduli i diferencës nuk priret në zero kur x→a. Por pastaj y nuk e arrin kufirin b në x→a, që bie ndesh me kushtet e teoremës.
Teorema 6. Nëse dy funksione f(x) Dhe g(x) për të gjitha vlerat e argumentit x kënaqin pabarazinë f(x)≥ g(x) dhe kanë kufij, atëherë qëndron pabarazia b≥c.
Dëshmi. Sipas kushteve të teoremës f(x)-g(x) ≥0, pra, nga teorema 5 ![]() , ose
, ose ![]() .
.
KUFIJT E NJËANËSHËM

Deri më tani kemi konsideruar përcaktimin e kufirit të një funksioni kur x→a në mënyrë arbitrare, d.m.th. kufiri i funksionit nuk varej nga mënyra se si ishte vendosur x drejt a, në të majtë ose në të djathtë të a. Sidoqoftë, është mjaft e zakonshme të gjesh funksione që nuk kanë kufi në këtë kusht, por ato kanë një kufi nëse x→a, duke mbetur në njërën anë të A, majtas ose djathtas (shih figurën). Prandaj, prezantohen konceptet e kufijve të njëanshëm.
Nëse f(x) priret në kufi b në x duke u përpjekur për një numër të caktuar a Kështu që x pranon vetëm vlera më të vogla se a, pastaj shkruajnë dhe thërrasin kufiri i funksionit f(x) në pikën a në të majtë.
Llogaritja e infinitezimaleve dhe të mëdhave
Njehsimi infinitimal- llogaritjet e kryera me madhësi infiniteminale, në të cilat rezultati i prejardhur konsiderohet si një shumë e pafundme infinitezimalesh. Llogaritja e infinitezimaleve është një koncept i përgjithshëm për llogaritjet diferenciale dhe integrale, i cili përbën bazën e matematikës së lartë moderne. Koncepti i një sasie infiniteminale është i lidhur ngushtë me konceptin e kufirit.
Pafundësisht i vogël
Pasoja a n thirrur pafundësisht i vogël, Nëse . Për shembull, një sekuencë numrash është pafundësisht e vogël.
Funksioni thirret pafundësisht i vogël në afërsi të një pike x 0 nëse ![]() .
.
Funksioni thirret pafundësisht i vogël në pafundësi, Nëse ![]() ose
ose ![]() .
.
Gjithashtu infinitezimal është një funksion që është ndryshimi midis një funksioni dhe kufirit të tij, domethënë nëse ![]() , Kjo f(x) − a = α( x)
, .
, Kjo f(x) − a = α( x)
, .
Sasi pafundësisht e madhe
Pasoja a n thirrur pafundësisht i madh, Nëse ![]() .
.
Funksioni thirret pafundësisht i madh në afërsi të një pike x 0 nëse ![]() .
.
Funksioni thirret pafundësisht i madh në pafundësi, Nëse ![]() ose
ose ![]() .
.
Në të gjitha rastet, pafundësia në të drejtën e barazisë nënkuptohet të ketë një shenjë të caktuar (ose "plus" ose "minus"). Ky është, për shembull, funksioni x mëkat x nuk është pafundësisht i madh në .
Vetitë e pafundësisht të vogla dhe pafundësisht të mëdha
Krahasimi i madhësive infiniteminale
Si të krahasoni sasitë infinite të vogla?
Raporti i sasive infiniteminale formon të ashtuquajturën pasiguri.
Përkufizimet
Supozoni se kemi vlera infiniteminale α( x) dhe β( x) (ose, që nuk është e rëndësishme për përkufizimin, sekuenca pafundësisht të vogla).
Për të llogaritur kufij të tillë është e përshtatshme të përdoret rregulli i L'Hopital.
Shembuj krahasues
Duke përdorur RRETH-simbolizmi, rezultatet e fituara mund të shkruhen në formën e mëposhtme x 5 = o(x 3). Në këtë rast, shënimet e mëposhtme janë të vërteta: 2x 2 + 6x = O(x) Dhe x = O(2x 2 + 6x).Vlerat ekuivalente
Përkufizimi
Nëse , atëherë quhen madhësitë infiniteminale α dhe β ekuivalente ().
Është e qartë se sasitë ekuivalente janë një rast i veçantë i sasive infiniteminale të rendit të njëjtë të vogëlsisë.
Kur relacionet e mëposhtme të ekuivalencës janë të vlefshme: , , ![]() .
.
Teorema
Kufiri i herësit (raportit) të dy sasive infiniteminale nuk do të ndryshojë nëse njëra prej tyre (ose të dyja) zëvendësohet nga një sasi ekuivalente..Kjo teoremë ka rëndësi praktike gjatë gjetjes së kufijve (shih shembullin).
Shembull përdorimi
Duke zëvendësuar sin 2x vlerë ekuivalente 2 x, marrimSkicë historike
Koncepti i "pafundësishëm" u diskutua në kohët e lashta në lidhje me konceptin e atomeve të pandarë, por nuk u përfshi në matematikën klasike. Ajo u ringjall përsëri me ardhjen e "metodës së të pandarëve" në shekullin e 16-të - duke e ndarë figurën në studim në seksione pafundësisht të vogla.
Në shekullin e 17-të, u bë algjebrizimi i llogaritjes infinitimale. Ato filluan të përkufizohen si madhësi numerike që janë më të vogla se çdo sasi e fundme (jo zero) dhe megjithatë nuk janë të barabarta me zero. Arti i analizës konsistonte në hartimin e një relacioni që përmban infinitezimale (diferenciale) dhe më pas integrimin e tij.
Matematikanët e shkollës së vjetër e vënë në provë konceptin pafundësisht i vogël kritika të ashpra. Michel Rolle shkroi se llogaritja e re është " grup gabimesh gjeniale"; Volteri vërejti në mënyrë kaustike se llogaritja është arti i llogaritjes dhe matjes së saktë të gjërave, ekzistenca e të cilave nuk mund të vërtetohet. Edhe Huygens pranoi se ai nuk e kuptonte kuptimin e diferencialeve të rendit më të lartë.
Mosmarrëveshjet në Akademinë e Shkencave të Parisit në lidhje me justifikimin e analizave u bënë aq skandaloze sa Akademia dikur i ndaloi plotësisht anëtarët e saj të flisnin për këtë temë (kjo kishte të bënte kryesisht me Rolle dhe Varignon). Në 1706 Rolle tërhoqi publikisht kundërshtimet e tij, por diskutimet vazhduan.
Në vitin 1734, filozofi i famshëm anglez, peshkopi George Berkeley, botoi një broshurë të bujshme, të njohur me titullin e shkurtuar " Analist" Emri i tij i plotë: " Një analist apo diskurs drejtuar matematikanit jobesimtar, ku pyetet nëse subjekti, parimet dhe përfundimet e analizës moderne perceptohen më qartë ose më qartë se sa sakramentet fetare dhe nenet e besimit».
Analisti përmbante një kritikë të mprehtë dhe kryesisht të drejtë të llogaritjes infinitimale. Berkeley e konsideroi metodën e analizës si të papajtueshme me logjikën dhe shkroi se, " sado e dobishme të jetë, mund të konsiderohet vetëm si një lloj hamendjeje; mjeshtëri e shkathët, art ose më mirë truk, por jo si metodë e provës shkencore" Duke cituar frazën e Njutonit për rritjen e sasive aktuale "në fillimin e origjinës ose zhdukjes së tyre", Berkeley me ironi: " ato nuk janë as sasi të fundme, as infinitezimale, madje as asgjë. A nuk mund t'i quajmë ata fantazmat e madhësive të vdekura?... Dhe si mund të flasim në përgjithësi për marrëdhëniet midis gjërave që nuk kanë madhësi? dallimi, nuk duhet, pasi më duket se gjej gabime me diçka në teologji».
Është e pamundur, shkruan Berkeley, të imagjinohet shpejtësia e menjëhershme, domethënë shpejtësia në një çast dhe në një pikë të caktuar, sepse koncepti i lëvizjes përfshin konceptet e hapësirës dhe kohës (të fundme jo zero).
Si jep analiza rezultate të sakta? Berkeley erdhi në idenë se kjo shpjegohej me praninë e disa gabimeve në përfundimet analitike, dhe e ilustron këtë me shembullin e një parabole. Është interesante që disa matematikanë të mëdhenj (për shembull, Lagrange) u pajtuan me të.
Një situatë paradoksale u ngrit kur ashpërsia dhe frytshmëria në matematikë ndërhynin me njëra-tjetrën. Pavarësisht përdorimit të veprimeve të paligjshme me koncepte të përcaktuara dobët, numri i gabimeve të drejtpërdrejta ishte çuditërisht i vogël - intuita erdhi në shpëtim. E megjithatë, gjatë gjithë shekullit të 18-të, analiza matematikore u zhvillua me shpejtësi, pa asnjë justifikim në thelb. Efikasiteti i tij ishte i mahnitshëm dhe foli vetë, por kuptimi i diferencialit ishte ende i paqartë. Rritja pafundësisht e vogël e një funksioni dhe pjesa e tij lineare shpesh ngatërroheshin.
Gjatë gjithë shekullit të 18-të, u bënë përpjekje të mëdha për të korrigjuar situatën, dhe matematikanët më të mirë të shekullit morën pjesë në to, por vetëm Cauchy arriti të ndërtojë bindshëm themelet e analizës në fillim të shekullit të 19-të. Ai përcaktoi rreptësisht konceptet themelore - kufiri, konvergjenca, vazhdimësia, diferenciali, etj., Pas së cilës infinitezimalet aktuale u zhdukën nga shkenca. Disa hollësi të mbetura u shpjeguan më vonë
Teorema 2.4. Nëse sekuencat (x n) dhe (y n) konvergojnë dhe x n ≤ y n, n > n 0, atëherë lim x n ≤ lim y n.
Le të lim xn = a, |
lim yn = b dhe a > b. Sipas përkufizimit 2.4 kufijtë |
||||||||||||||||||||
sekuencat sipas numrit ε = |
ekziston një numër N i tillë që |
||||||||||||||||||||
Prandaj, n > max(n0, N) yn< |
< xn , что противоречит |
||||||||||||||||||||
gjendje. |
|||||||||||||||||||||
Koment. Nëse sekuencat (xn), (yn) konvergojnë për |
|||||||||||||||||||||
të gjitha n > n0 |
xn< yn , то можно утверждать лишь, что lim xn |
≤ lim yn . |
|||||||||||||||||||
Për ta parë këtë, mjafton të merren parasysh sekuencat
dhe yn = |
||||
Rezultatet e mëposhtme rrjedhin drejtpërdrejt nga Përkufizimi 2.4.
Teorema 2.5. Nëse sekuenca e numrave (x n) konvergon dhe lim x n< b (b R), то N N: x n < b, n >N.
Pasoja. Nëse sekuenca (xn) konvergon dhe lim xn 6= 0, atëherë
N N: sgn xn = sgn(lim xn), n > N.
Teorema 2.6. Lërini sekuencat (x n), (y n), (z n) të plotësojnë kushtet:
1) x n ≤ yn ≤ zn , n > n0 ,
2) sekuencat(x n) dhe (z n) konvergojnë dhe lim x n = lim z n = a.
Pastaj sekuenca (y n ) konvergon dhe lim y n = a.
2.1.3 Sekuenca pafundësisht të vogla
Përkufizimi 2.7. Një sekuencë numrash (x n) quhet infinite vogël (infinite vogël) nëse konvergon dhe lim x n = 0.
Sipas përkufizimit 2.4 të kufirit të një sekuence numrash, përkufizimi 2.7 është ekuivalent me sa vijon:
Përkufizimi 2.8. Një sekuencë numerike (x n) quhet infinitimale nëse për çdo numër pozitiv ε ekziston një numër N = N(ε) i tillë që për të gjithë n > N elementet x n të kësaj sekuence plotësojnë pabarazinë |x n |< ε.
Pra, (xn) - b.m. ε > 0 N = N(ε) : n > N |xn |< ε.
Nga Shembujt 2, 3 dhe Vërejtja 1 deri te Teorema 2.3 marrim se pas
vlefshmëria ( |
q−n |
janë të pafundme |
||||||||||||
Vetitë e sekuencave infiniteminale përshkruhen nga teoremat e mëposhtme.
Teorema 2.7. Shuma e një numri të fundëm të sekuencave infinitimale është një sekuencë infinite vogël.
Le të jenë të pafundme sekuencat (xn), (yn). Le të tregojmë se (xn + yn) do të jetë gjithashtu një. Le të vendosim ε > 0. Pastaj ka një numër
N1 = N1 (ε) i tillë që |
||||
|xn |< |
N>N1, |
|||
dhe ka një numër N2 = N2 (ε) i tillë që |
||||
|yn |< |
N>N2. |
|||
Le të shënojmë me N = max(N1, N2). Për n > N, pabarazitë (2.1) dhe (2.2) do të jenë të vlefshme. Prandaj, për n > N
|xn + yn | ≤ |xn | + |yn |< 2 + 2 = ε.
Kjo do të thotë se sekuenca (xn +yn) është infinitimale. Deklaratë për shumën e një numri të fundëm të sekuencave infiniteminale
Kjo rrjedh nga ajo që u vërtetua me induksion.
Teorema 2.8. Prodhimi i një sekuence infinite vogël dhe i një sekuence të kufizuar është infinite vogël.
Le të jetë (xn) një sekuencë e kufizuar dhe (yn) një sekuencë infiniteminale. Sipas përkufizimit 2.6 të një sekuence të kufizuar ekziston një numër M > 0 i tillë që
|xn | ≤ M, n N. |
Le të rregullojmë një numër arbitrar ε > 0. Meqenëse (yn) është një sekuencë infinite vogël, ekziston një numër N = N(ε) i tillë që
Prandaj, sekuenca (xn yn ) është pafundësisht i vogël.

Përfundim 1. Prodhimi i një sekuence infinite vogël dhe një sekuence konvergjente është një sekuencë infinite vogël.
Përfundim 2. Prodhimi i dy sekuencave infinitimale është një sekuencë infinite vogël.
Duke përdorur sekuenca pafundësisht të vogla, përkufizimi i një sekuence konvergjente mund të shihet ndryshe.
Lema 2.1. Në mënyrë që numri a të jetë kufiri i sekuencës numerike (x n), është e nevojshme dhe e mjaftueshme që të ketë një paraqitje x n = a + α n, n N, në të cilën (α n) është një sekuencë infiniteminale.
Domosdoshmëri. Le të lim xn = a dhe a R. Pastaj
ε > 0 N = N(ε) N: n > N |xn − a|< ε.
Nëse vendosim αn = xn − a, n N, atëherë marrim se (αn) është një sekuencë infiniteminale dhe xn = a + αn, n N.
Përshtatshmëria. Le të jetë sekuenca (xn) e tillë që ekziston një numër a për të cilin xn = a + αn, n N dhe lim αn = 0. Le të rregullojmë një numër arbitrar pozitiv ε. Meqenëse lim αn = 0, atëherë ekziston një numër N = N(ε) N i tillë që |αn |< ε, n >N. Kjo do të thotë, në shënimet e tjera, n > N |xn − a|< ε. Это означает, что lim xn = a.
Le të zbatojmë Lemën 2.1 për një shembull të veçantë të rëndësishëm.
Lema 2.2. lim n n = 1.
√ √
Meqenëse për të gjitha n > 1 n n > 1, atëherë n n = 1 + αn , dhe αn > 0 për
të gjitha n > 1. Prandaj n = (1 + α |
)n = 1 + nα |
+ αn. |
|||||||||||||||
Meqenëse të gjithë termat janë pozitivë, n |
|||||||||||||||||
Le të jetë ε > 0. Meqenëse |
2/n< ε для всех n >2/ε , atëherë, duke supozuar |
||||||||||||||||
N = max (1, ), marrim se 0< αn < ε, n >N. Prandaj,
sekuenca (αn) është pafundësisht e vogël dhe, sipas lemës
2.1, lim n n = 1. √
Pasoja. Nëse a > 1, atëherë lim n a = 1.√ √
Deklarata rrjedh nga pabarazitë 1< n a ≤ n n , n >[a].
2.1.4 Veprimet aritmetike me sekuenca
Duke përdorur Lemën 2.1 dhe vetitë e sekuencave infiniteminale, është e lehtë të përftohen teorema mbi kufijtë e sekuencave të marra duke përdorur veprime aritmetike nga sekuencat konvergjente.

|b| 3|b|
2 < |y n | < 2
Teorema 2.9. Le të konvergojnë sekuencat e numrave (x n) dhe (y n). Atëherë mbahen deklaratat e mëposhtme:
1) sekuenca (x n ± y n ) konvergon dhe
lim(xn ± yn) = lim xn ± lim yn;
2) sekuenca (x n · y n ) konvergon dhe
lim(xn · yn) = lim xn · lim yn;
3) nëse lim y n 6= 0, atëherë raporti x n /y n përcaktohet duke filluar nga
disa numra, sekuenca ( x n ) konvergon dhe
Nga teorema 2.8 dhe përfundimi 1, sekuencat (a · βn), (b · αn), (αn · βn) janë pafundësisht të vogla. Nga teorema 2.7, sekuenca (aβn + bαn + αn βn ) është infiniteminale. Deklarata 2) rrjedh nga përfaqësimi (2.5) nga Lema 2.1.
Le të kthehemi te pohimi 3). Sipas kushtit, lim yn = b 6= 0. Në bazë të teoremës 2.3. sekuenca (|yn |) konvergon dhe lim |yn | = |b| 6= 0. Prandaj, duke pasur parasysh numrin ε = |b|/2, ekziston një numër N i tillë që n > N
0 < | 2 b| = |b| −
Prandaj, yn =6 0, dhe 3|b|< y n < |b| , n >N.
Kështu, herësi xn /yn përcaktohet për të gjitha n > N, dhe sekuenca (1/yn) është e kufizuar. Merrni parasysh për të gjitha n > N ndryshimin
(αn b − aβn ). |
|||||||||||||||||||||
Pasoja |
αn b |
aβn |
Pafundësisht i vogël |
||||||||||||||||||
kufizuar. Nga teorema 2.8 sekuenca |
|||||||||||||||||||||
− b |
|||||||||||||||||||||
shumë i vogël. Prandaj, nga Lema 2.1, pohimi 3) vërtetohet. Përfundim 1. Nëse sekuenca (xn) konvergon, atëherë për ndonjë
Për çdo numër c, sekuenca (c · xn ) konvergon dhe lim(cxn) = c · lim xn.
Funksionet infiniteminale
Funksioni %%f(x)%% thirret pafundësisht i vogël(b.m.) me %%x \në një \in \overline(\mathbb(R))%%, nëse me këtë tendencë të argumentit kufiri i funksionit është i barabartë me zero.
Koncepti i b.m. funksioni është i lidhur pazgjidhshmërisht me udhëzimet për të ndryshuar argumentin e tij. Mund të flasim për b.m. funksionon në %%a \në a + 0%% dhe në %%a \në a - 0%%. Zakonisht b.m. funksionet shënohen me shkronjat e para të alfabetit grek %%\alpha, \beta, \gama, \ldots%%
Shembuj
- Funksioni %%f(x) = x%% është b.m. në %%x \në 0%%, pasi kufiri i tij në pikën %%a = 0%% është zero. Sipas teoremës për lidhjen ndërmjet kufirit dy anësor dhe kufirit të njëanshëm, ky funksion është b.m. si me %%x \në +0%% dhe me %%x \në -0%%.
- Funksioni %%f(x) = 1/(x^2)%% - b.m. në %%x \në \infty%% (si dhe në %%x \në +\infty%% dhe në %%x \në -\infty%%).
Një numër konstant jo zero, sado i vogël në vlerë absolute, nuk është një b.m. funksionin. Për numrat konstante, përjashtimi i vetëm është zero, pasi funksioni %%f(x) \equiv 0%% ka një kufi zero.
Teorema
Funksioni %%f(x)%% ka në pikën %%a \in \overline(\mathbb(R))%% të vijës numerike të zgjeruar një kufi përfundimtar të barabartë me numrin %%b%% nëse dhe vetëm nëse ky funksion është i barabartë me shumën e këtij numri %%b%% dhe b.m. funksionet %%\alpha(x)%% me %%x \në a%%, ose $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R ) \Shigjeta majtas \majtë(f(x) = b + \alfa(x)\djathtas) \land \left(\lim\limits_(x \to a)(\alfa(x) = 0)\djathtas). $$
Vetitë e funksioneve infiniteminale
Sipas rregullave të kalimit në kufirin me %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%%, vijojnë pohimet e mëposhtme:
- Shuma e numrit përfundimtar të b.m. funksionet për %%x \në a%% është b.m. në %%x \në një%%.
- Prodhimi i çdo numri b.m. funksionet për %%x \në a%% është b.m. në %%x \në një%%.
Produkti b.m. funksionon në %%x \në a%% dhe një funksion i kufizuar në ndonjë lagje të shpuar %%\stackrel(\circ)(\text(U))(a)%% e pikës a, ka b.m. në funksionin %%x \në a%%.
Është e qartë se prodhimi i një funksioni konstant dhe b.m. në %%x \në a%% ka b.m. funksion në %%x \në një%%.
Funksionet ekuivalente infiniteminale
Funksionet pafundësisht të vogla %%\alfa(x), \beta(x)%% për %%x \në a%% quhen ekuivalente dhe shkruani %%\alfa(x) \sim \beta(x)%%, nëse
$$ \lim\limits_(x \në a)(\frac(\alfa(x))(\beta(x)) = \lim\limits_(x \në a)(\frac(\beta(x) )(\alfa(x))) = 1. $$
Teorema mbi zëvendësimin e b.m. funksionet ekuivalente
Le të jetë %%\alfa(x), \alpha_1(x), \beta(x), \beta_1(x)%% b.m. funksionet për %%x \në a%%, me %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, pastaj $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x)) = \lim\ limitet_(x \në a)(\frac(\alfa_1(x))(\beta_1(x))). $$
Ekuivalente b.m. funksione.
Le të jetë %%\alfa(x)%% b.m. funksion në %%x \në a%%, atëherë
- %%\sin(\alfa(x)) \sim \alpha(x)%%
- %%\stil ekrani 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
- %%\tan \alfa(x) \sim \alpha(x)%%
- %%\arcsin\alpha(x) \sim \alpha(x)%%
- %%\arctan\alpha(x) \sim \alpha(x)%%
- %%\ln(1 + \alfa(x)) \sim \alfa(x)%%
- %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
- %%\displaystyle a^(\alpha(x)) - 1 \sim \alpha(x) \ln(a)%%
Shembull
$$ \begin(array)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \në 0)(\frac(\ln(1 + (\cos x - 1)))(\frac(x^2)(4)) = \\ & = \lim\ limits_(x \to 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\ limits_(x \deri 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \fund (array) $$
Funksione pafundësisht të mëdha
Funksioni %%f(x)%% thirret pafundësisht i madh(b.b.) me %%x \në një \in \overline(\mathbb(R))%%, nëse me këtë tendencë të argumentit funksioni ka një kufi të pafund.
Ngjashëm me b.m. koncepti i funksioneve b.b. funksioni është i lidhur pazgjidhshmërisht me udhëzimet për të ndryshuar argumentin e tij. Mund të flasim për b.b. funksionon me %%x \në a + 0%% dhe %%x \në a - 0%%. Termi "pafundësisht i madh" nuk flet për vlerën absolute të funksionit, por për natyrën e ndryshimit të tij në afërsi të pikës në fjalë. Asnjë numër konstant, sado i madh në vlerë absolute, nuk është pafundësisht i madh.
Shembuj
- Funksioni %%f(x) = 1/x%% - b.b. në %%x \në 0%%.
- Funksioni %%f(x) = x%% - b.b. në %%x \në \infty%%.
Nëse përkufizimi kushtëzon $$ \begin(array)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)(f( x)) = -\infty, \end(array) $$
pastaj flasin për pozitive ose negativ b.b. në funksionin %%a%%.
Shembull
Funksioni %%1/(x^2)%% - pozitiv b.b. në %%x \në 0%%.
Lidhja ndërmjet b.b. dhe b.m. funksione
Nëse %%f(x)%% është b.b. me funksionin %%x \në a%%, pastaj %%1/f(x)%% - b.m.
në %%x \në një%%. Nëse %%\alfa(x)%% - b.m. sepse %%x \në a%% është një funksion jo zero në disa lagje të shpuara të pikës %%a%%, atëherë %%1/\alfa(x)%% është b.b. në %%x \në një%%.
Vetitë e funksioneve pafundësisht të mëdha
Le të paraqesim disa veti të b.b. funksione. Këto veti rrjedhin drejtpërdrejt nga përkufizimi i b.b. funksionet dhe vetitë e funksioneve që kanë kufij të fundëm, si dhe nga teorema mbi lidhjen ndërmjet b.b. dhe b.m. funksione.
- Prodhimi i një numri të fundëm të b.b. funksionet për %%x \në a%% është b.b. funksion në %%x \në një%%. Në të vërtetë, nëse %%f_k(x), k = \overline(1, n)%% - b.b. funksionon në %%x \në a%%, pastaj në një lagje të shpuar të pikës %%a%% %%f_k(x) \ne 0%%, dhe nga teorema e lidhjes b.b. dhe b.m. funksionet %%1/f_k(x)%% - b.m. funksion në %%x \në një%%. Rezulton %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% - b.m funksion për %%x \në a%%, dhe %%\displaystyle\prod^(n )_(k = 1)f_k(x)%% - b.b. funksion në %%x \në një%%.
- Produkti b.b. funksionet për %%x \në a%% dhe një funksion i cili në një lagje të shpuar të pikës %%a%% në vlerë absolute është më i madh se një konstante pozitive është b.b. funksion në %%x \në një%%. Në veçanti, produkti b.b. një funksion me %%x \në a%% dhe një funksion që ka një kufi të fundëm jozero në pikën %%a%% do të jetë b.b. funksion në %%x \në një%%.
Shuma e dy b.b. funksionon në %%x \në a%% ka pasiguri. Në varësi të shenjës së termave, natyra e ndryshimit në një shumë të tillë mund të jetë shumë e ndryshme.
Shembull
Le të jepen funksionet %%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%%. funksionon në %%x \në \infty%%. Pastaj:
- %%f(x) + g(x) = 3x%% - b.b. funksion në %%x \në \infty%%;
- %%f(x) + h(x) = 0%% - b.m. funksion në %%x \në \infty%%;
- %%h(x) + v(x) = \sin x%% nuk ka kufi në %%x \në \infty%%.
Shuma e një funksioni të kufizuar në një lagje të shpuar të pikës %%a%% dhe b.b. funksionet me %%x \në a%% është b.b. funksion në %%x \në një%%.
Për shembull, funksionet %%x - \sin x%% dhe %%x + \cos x%% janë b.b. në %%x \në \infty%%.
