Infinitesimal ketma-ketliklar - ta'rifi va xususiyatlari. Misollar Qanday miqdor cheksiz kichik deb ataladi
Cheksiz kichiklar va kattalar hisobi
Cheksiz kichik hisob- cheksiz kichik qiymatlar bilan bajariladigan hisoblar, bunda olingan natija cheksiz kichiklarning cheksiz yig'indisi sifatida qaraladi. Cheksiz kichiklar hisobi zamonaviy oliy matematikaning asosini tashkil etuvchi differentsial va integral hisoblar uchun umumiy tushunchadir. Cheksiz kichik miqdor tushunchasi chegara tushunchasi bilan chambarchas bog'liq.
Cheksiz kichik
Keyingi ketma-ketlik a n chaqirdi cheksiz kichik, Agar . Masalan, raqamlar ketma-ketligi cheksiz kichikdir.
Funktsiya chaqiriladi nuqta qo'shnisida cheksiz kichik x 0 agar ![]() .
.
Funktsiya chaqiriladi cheksizlikda cheksiz kichik, Agar ![]() yoki
yoki ![]() .
.
Shuningdek, cheksiz kichik funktsiya va uning chegarasi o'rtasidagi farq, ya'ni agar ![]() , Bu f(x) − a = α( x)
, .
, Bu f(x) − a = α( x)
, .
cheksiz katta
Quyidagi barcha formulalarda tenglikning o'ng tomonidagi cheksizlik ma'lum bir belgini nazarda tutadi (yoki "ortiqcha" yoki "minus"). Bu, masalan, funktsiya x gunoh x, har ikki tomondan chegaralanmagan, uchun cheksiz katta emas.
Keyingi ketma-ketlik a n chaqirdi cheksiz katta, Agar ![]() .
.
Funktsiya chaqiriladi nuqta qo'shnisida cheksiz katta x 0 agar ![]() .
.
Funktsiya chaqiriladi cheksizlikda cheksiz katta, Agar ![]() yoki
yoki ![]() .
.
Cheksiz va cheksiz kichiklarning xossalari
Cheksiz kichiklarni solishtirish
Cheksiz kichik miqdorlarni qanday solishtirish mumkin?
Cheksiz kichik miqdorlarning nisbati noaniqlik deb ataladigan narsani hosil qiladi.
Ta'riflar
Aytaylik, bizda bir xil qiymat uchun cheksiz kichik a( x) va b( x) (yoki ta'rif uchun muhim bo'lmagan, cheksiz kichik ketma-ketliklar).
Bunday chegaralarni hisoblash uchun L'Hospital qoidasidan foydalanish qulay.
Taqqoslash misollari
Foydalanish HAQIDA-olingan natijalarning belgilarini quyidagi shaklda yozish mumkin x 5 = o(x 3). Bunday holda, yozuvlar 2x 2 + 6x = O(x) Va x = O(2x 2 + 6x).Ekvivalent miqdorlar
Ta'rif
Agar , u holda cheksiz kichik miqdorlar a va b deyiladi ekvivalent ().
Shubhasiz, ekvivalent miqdorlar bir xil kichiklik tartibidagi cheksiz kichik miqdorlarning alohida holatidir.
, uchun quyidagi ekvivalentlik munosabatlari mavjud (e'tiborli chegaralar deb ataladigan narsa natijasida):
Teorema
Ikki cheksiz kichik miqdorning chegarasi (nisbati) agar ulardan biri (yoki ikkalasi) ekvivalent qiymat bilan almashtirilsa, o'zgarmaydi..Bu teorema chegaralarni topishda amaliy ahamiyatga ega (misolga qarang).
Foydalanish misoli
O'zgartirish sin 2x ekvivalent qiymat 2 x, olamizTarixiy tasavvur
“Cheksiz kichik” tushunchasi qadimgi davrlarda boʻlinmas atomlar tushunchasi bilan bogʻliq holda muhokama qilingan, ammo klassik matematikaga kirmagan. Yana 16-asrda “boʻlinmaslar usuli” – oʻrganilayotgan figuraning cheksiz kichik boʻlimlarga boʻlinishi paydo boʻlishi bilan qayta tiklandi.
Cheksiz kichik hisobni algebralash XVII asrda sodir bo'lgan. Ular har qanday chekli (nol bo'lmagan) qiymatdan kichik bo'lgan va nolga teng bo'lmagan raqamli qiymatlar sifatida aniqlana boshladilar. Tahlil san'ati cheksiz kichiklarni (differensiallarni) o'z ichiga olgan munosabatni tuzishdan, keyin esa uni integrallashdan iborat edi.
Qadimgi maktab matematiklari kontseptsiyaga bo'ysundilar cheksiz kichik qattiq tanqid. Mishel Rol yangi hisob-kitoblar " ajoyib xatolar to'plami»; Volter bu hisob borligini isbotlab bo'lmaydigan narsalarni hisoblash va to'g'ri o'lchash san'ati ekanligini qattiq ta'kidladi. Hatto Gyuygens ham yuqori tartibli differentsiallarning ma'nosini tushunmaganligini tan oldi.
Taqdirning istehzosi sifatida asrning o'rtalarida paydo bo'lgan nostandart tahlilni ko'rib chiqish mumkin, bu esa asl nuqtai nazar - haqiqiy cheksiz kichiklarning ham izchilligini isbotladi va tahlil qilish uchun asos sifatida qabul qilinishi mumkin.
Shuningdek qarang
Wikimedia fondi. 2010 yil.
Boshqa lug'atlarda "Infinitesimal" nima ekanligini ko'ring:
CHEKSIZ KICHIK- ba'zi bir jarayondagi o'zgaruvchi, agar bu jarayonda u cheksiz ravishda nolga yaqinlashsa (moyil bo'lsa) ... Katta politexnika entsiklopediyasi
cheksiz kichik- ■ Noma'lum narsa, lekin gomeopatiya bilan bog'liq... Umumiy haqiqatlar leksikasi
CHEKSIZ KICHIK FUNKSIYALAR VA ULARNING ASOSIY XUSUSIYATLARI
Funktsiya y=f(x) chaqirdi cheksiz kichik da x→a yoki qachon x→∞ agar yoki bo'lsa, ya'ni. Cheksiz kichik funktsiya - berilgan nuqtadagi chegarasi nolga teng bo'lgan funksiya.
Misollar.
Keling, quyidagi muhim munosabatni o'rnatamiz:
Teorema. Agar funktsiya y=f(x) da vakili mumkin x→a doimiy sonning yig'indisi sifatida b va cheksiz kichik a(x): f(x)=b+ a(x) Bu .
Aksincha, agar , keyin f(x)=b+a(x), Qayerda a(x) da cheksiz kichikdir x→a.
Isbot.
Cheksiz kichik funksiyalarning asosiy xossalarini ko'rib chiqamiz.
Teorema 1. Ikki, uch va umuman har qanday chekli sonli cheksiz kichiklarning algebraik yig‘indisi cheksiz kichik funktsiyadir.
Isbot. Keling, ikkita atama uchun dalil keltiraylik. Mayli f(x)=a(x)+b(x), qayerda va . Biz buni isbotlashimiz kerak ixtiyoriy ixtiyoriy kichik e uchun > 0 bor δ> 0, shuning uchun x tengsizlikni qondirish |x – a|<δ , bajarildi |f(x)|< ε.
Shunday qilib, biz ixtiyoriy e raqamini tuzatamiz > 0. Chunki teorema gipotezasiga ko'ra, a(x) cheksiz kichik funktsiya bo'lsa, u holda d 1 mavjud > 0, qaysi da |x – a|< d 1 bizda bor |a(x)|< ε / 2. Xuddi shunday, beri b(x) cheksiz kichik bo'lsa, unda shunday d 2 mavjud > 0, qaysi da |x – a|< d 2 bizda bor | b(x)|< ε / 2.
Keling, olamiz d=min( d1 , d2 } .Keyin nuqtaning bir mahallasida a radius δ tengsizliklarning har biri qanoatlantiriladi |a(x)|< ε / 2 va | b(x)|< ε / 2. Shuning uchun, bu mahallada bo'ladi
|f(x)|=| a(x)+b(x)| ≤ |a(x)| + | b(x)|< ε /2 + ε /2= ε,
bular. |f(x)|< e, bu isbotlanishi kerak edi.
Teorema 2. Cheksiz kichik funktsiyaning mahsuloti a(x) cheklangan funksiya uchun f(x) da x→a(yoki qachon x→∞) cheksiz kichik funksiyadir.
Isbot. Funktsiyadan beri f(x) cheklangan, keyin raqam bor M Shunday qilib, barcha qadriyatlar uchun x nuqtaning qaysidir mahallasidan a|f(x)|≤M. Bundan tashqari, beri a(x) uchun cheksiz kichik funktsiyadir x→a, keyin ixtiyoriy e uchun > 0 nuqtaning qo'shnisi bor a, unda tengsizlik |a(x)|< ε /M. Keyin bu kichikroq mahallalarda bizda bor | af|< ε /M= e. Va bu shuni anglatadiki af- cheksiz kichik. Ish uchun x→∞ isbotlash xuddi shunday tarzda amalga oshiriladi.
Tasdiqlangan teoremadan kelib chiqadi:
Natija 1. Agar va bo'lsa, u holda.
Natija 2. Agar c= const, keyin .
Teorema 3. Cheksiz kichik funktsiyaning nisbati a(x) har bir funktsiya uchun f(x) chegarasi nolga teng bo‘lmagan , cheksiz kichik funksiyadir.
Isbot. Mayli ![]() . Keyin 1 /f(x) cheklangan funksiya mavjud. Shuning uchun kasr
. Keyin 1 /f(x) cheklangan funksiya mavjud. Shuning uchun kasr ![]() cheksiz kichik funktsiya va chegaralangan funktsiyaning mahsulotidir, ya'ni. funksiya cheksiz kichikdir.
cheksiz kichik funktsiya va chegaralangan funktsiyaning mahsulotidir, ya'ni. funksiya cheksiz kichikdir.
CHEKSIZ KICHIK VA CHEKSIZ KATTA FUNKSIYALAR O'RTASIDAGI MUNOSABAT
Teorema 1. Agar funktsiya f(x) da cheksiz katta x→a, keyin funksiya 1 /f(x) da cheksiz kichikdir x→a.
Isbot. Ixtiyoriy e raqamini oling >0 va buni ba'zilarga ko'rsating δ>0 (e ga qarab) hamma uchun x, buning uchun |x – a|<δ , tengsizlik qanoatlantiriladi va bu shuni bildiradi 1/f(x) cheksiz kichik funksiyadir. Haqiqatan ham, beri f(x) uchun cheksiz katta funksiyadir x→a, keyin bor δ>0 tez orada shunday |x – a|<δ , shuning uchun | f(x)|> 1/ e. Ammo keyin xuddi shu uchun x.
Misollar.
Qarama-qarshi teorema ham isbotlanishi mumkin.
Teorema 2. Agar funktsiya f(x)- cheksiz kichik da x→a(yoki x→∞) va keyin yo'qolmaydi y= 1/f(x) cheksiz funksiyadir.
Teoremani o'zingiz isbotlang.
Misollar.
Shunday qilib, cheksiz kichik va cheksiz katta funksiyalarning eng oddiy xossalarini quyidagi shartli munosabatlar yordamida yozish mumkin: A≠ 0
HAQIDA TEOREMALAR
Teorema 1. Ikki, uchta va umuman ma'lum miqdordagi funktsiyalarning algebraik yig'indisining chegarasi bu funktsiyalar chegaralarining algebraik yig'indisiga teng, ya'ni.
Isbot. Biz isbotni ikki muddat uchun bajaramiz, chunki istalgan sonli atamalar uchun u xuddi shu tarzda amalga oshiriladi. Mayli ![]() .Keyin f(x)=b+a(x) Va g(x)=c+b(x), Qayerda α
Va β
cheksiz kichik funksiyalardir. Demak,
.Keyin f(x)=b+a(x) Va g(x)=c+b(x), Qayerda α
Va β
cheksiz kichik funksiyalardir. Demak,
f(x) + g(x)=(b + c) + (a(x) + b(x)).
Chunki b+c doimiy hisoblanadi, va a(x) + b(x) u cheksiz kichik funktsiyadir
Misol. .
Teorema 2. Ikki, uch va umuman, chekli sonli funksiyalar ko‘paytmasining chegarasi ushbu funksiyalar chegaralarining ko‘paytmasiga teng:
Isbot. Mayli ![]() . Demak, f(x)=b+a(x) Va g(x)=c+b(x) Va
. Demak, f(x)=b+a(x) Va g(x)=c+b(x) Va
fg = (b + a)(c + b) = bc + (bb + ca + ab).
Ish miloddan avvalgi doimiy qiymatdir. Funktsiya bb + ca + ab cheksiz kichik funksiyalar xossalari asosida cheksiz kichik miqdor mavjud. Shunung uchun .
Natija 1. Doimiy omil chegara belgisidan chiqarilishi mumkin:
![]() .
.
Natija 2. Darajaning chegarasi chegara darajasiga teng:
![]() .
.
Misol.![]() .
.
Teorema 3. Ikki funktsiyaning bo'linmasining chegarasi, agar maxrajning chegarasi noldan farqli bo'lsa, bu funktsiyalar chegaralarining ko'rsatkichiga teng bo'ladi, ya'ni.
 .
.
Isbot. Mayli. Demak, f(x)=b+a(x) Va g(x)=c+b(x), Qayerda α, β cheksiz kichikdir. Ko'rsatkichni ko'rib chiqing
Kasr cheksiz kichik funktsiyadir, chunki pay cheksiz kichik funktsiyadir va maxraj chegarasiga ega. c2 ≠0.
Misollar.

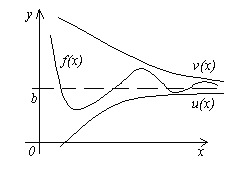
Teorema 4. Uchta funktsiya berilsin f(x), u(x) Va v(x), u tengsizliklarni qanoatlantirish (x)≤f(x)≤v(x). Funktsiyalar bo'lsa u(x) Va v(x) bir xil chegaraga ega x→a(yoki x→∞), keyin funksiya f(x) bir xil chegaraga intiladi, ya'ni. Agar
![]() , Bu.
, Bu.
Ushbu teoremaning ma'nosi rasmdan aniq.
4-teoremaning isbotini, masalan, darslikdan topish mumkin: Piskunov N. S. Differensial va integral hisoblar, 1-jild - M .: Nauka, 1985.
Teorema 5. Agar da x→a(yoki x→∞) funktsiyasi y=f(x) manfiy bo'lmagan qiymatlarni oladi y≥0 va chegaraga intiladi b, u holda bu chegara salbiy bo'lishi mumkin emas: b≥0.
Isbot. Isbot qarama-qarshilik bilan amalga oshiriladi. Keling, shunday da'vo qilaylik b<0 , Keyin |y – b|≥|b| va shuning uchun farq moduli da nolga moyil emas x→a. Ammo keyin y chegaraga chiqmaydi b da x→a, bu teorema shartiga ziddir.
Teorema 6. Ikki funktsiya bo'lsa f(x) Va g(x) argumentning barcha qiymatlari uchun x tengsizlikni qanoatlantiring f(x)≥ g(x) va chegaralari bo'lsa, biz tengsizlikka egamiz b≥c.
Isbot. Teorema bo'yicha f(x)-g(x) ≥0, shuning uchun 5-teorema bo'yicha ![]() , yoki
, yoki ![]() .
.
BIR TARAFLI CHEKLAMALAR

Hozirgacha funksiya limitining ta'rifini qachon ko'rib chiqdik x→a o'zboshimchalik bilan, ya'ni. funktsiyaning chegarasi qanday bo'lishiga bog'liq emas edi x munosabatga ko'ra a, chapga yoki o'ngga a. Biroq, bu shartda chegarasi bo'lmagan funktsiyalarni topish juda keng tarqalgan, ammo ularda chegara mavjud x→a, bir tomonida qolish A, chap yoki o'ng (rasmga qarang). Shuning uchun bir tomonlama chegaralar tushunchasi kiritiladi.
Agar f(x) chegaraga intiladi b da x qandaydir raqamga intilish a shunday qilib x dan kichik qiymatlarni qabul qiladi a, keyin yozing va qo'ng'iroq qiling f(x) funksiyaning chap tomondagi a nuqtadagi chegarasi.
Cheksiz kichiklar va kattalar hisobi
Cheksiz kichik hisob- cheksiz kichik qiymatlar bilan bajariladigan hisoblar, bunda olingan natija cheksiz kichiklarning cheksiz yig'indisi sifatida qaraladi. Cheksiz kichiklar hisobi zamonaviy oliy matematikaning asosini tashkil etuvchi differentsial va integral hisoblar uchun umumiy tushunchadir. Cheksiz kichik miqdor tushunchasi chegara tushunchasi bilan chambarchas bog'liq.
Cheksiz kichik
Keyingi ketma-ketlik a n chaqirdi cheksiz kichik, Agar . Masalan, raqamlar ketma-ketligi cheksiz kichikdir.
Funktsiya chaqiriladi nuqta qo'shnisida cheksiz kichik x 0 agar ![]() .
.
Funktsiya chaqiriladi cheksizlikda cheksiz kichik, Agar ![]() yoki
yoki ![]() .
.
Shuningdek, cheksiz kichik funktsiya va uning chegarasi o'rtasidagi farq, ya'ni agar ![]() , Bu f(x) − a = α( x)
, .
, Bu f(x) − a = α( x)
, .
cheksiz katta
Keyingi ketma-ketlik a n chaqirdi cheksiz katta, Agar ![]() .
.
Funktsiya chaqiriladi nuqta qo'shnisida cheksiz katta x 0 agar ![]() .
.
Funktsiya chaqiriladi cheksizlikda cheksiz katta, Agar ![]() yoki
yoki ![]() .
.
Barcha holatlarda tenglik huquqining cheksizligi ma'lum bir belgiga ega deb hisoblanadi (yoki "ortiqcha" yoki "minus"). Bu, masalan, funktsiya x gunoh x uchun cheksiz katta emas.
Cheksiz va cheksiz kichiklarning xossalari
Cheksiz kichiklarni solishtirish
Cheksiz kichik miqdorlarni qanday solishtirish mumkin?
Cheksiz kichik miqdorlarning nisbati noaniqlik deb ataladigan narsani hosil qiladi.
Ta'riflar
Aytaylik, bizda bir xil qiymat uchun cheksiz kichik a( x) va b( x) (yoki ta'rif uchun muhim bo'lmagan, cheksiz kichik ketma-ketliklar).
Bunday chegaralarni hisoblash uchun L'Hospital qoidasidan foydalanish qulay.
Taqqoslash misollari
Foydalanish HAQIDA-olingan natijalarning belgilarini quyidagi shaklda yozish mumkin x 5 = o(x 3). Bunday holda, yozuvlar 2x 2 + 6x = O(x) Va x = O(2x 2 + 6x).Ekvivalent miqdorlar
Ta'rif
Agar , u holda cheksiz kichik miqdorlar a va b deyiladi ekvivalent ().
Shubhasiz, ekvivalent miqdorlar bir xil kichiklik tartibidagi cheksiz kichik miqdorlarning alohida holatidir.
uchun quyidagi ekvivalentlik munosabatlari o’rinlidir: , , ![]() .
.
Teorema
Ikki cheksiz kichik miqdorning chegarasi (nisbati) agar ulardan biri (yoki ikkalasi) ekvivalent qiymat bilan almashtirilsa, o'zgarmaydi..Bu teorema chegaralarni topishda amaliy ahamiyatga ega (misolga qarang).
Foydalanish misoli
O'zgartirish sin 2x ekvivalent qiymat 2 x, olamizTarixiy tasavvur
“Cheksiz kichik” tushunchasi qadimgi davrlarda boʻlinmas atomlar tushunchasi bilan bogʻliq holda muhokama qilingan, ammo klassik matematikaga kirmagan. Yana 16-asrda “boʻlinmaslar usuli” – oʻrganilayotgan figuraning cheksiz kichik boʻlimlarga boʻlinishi paydo boʻlishi bilan qayta tiklandi.
Cheksiz kichik hisobni algebralash XVII asrda sodir bo'lgan. Ular har qanday chekli (nol bo'lmagan) qiymatdan kichik bo'lgan va nolga teng bo'lmagan raqamli qiymatlar sifatida aniqlana boshladilar. Tahlil san'ati cheksiz kichiklarni (differensiallarni) o'z ichiga olgan munosabatni tuzishdan, keyin esa uni integrallashdan iborat edi.
Qadimgi maktab matematiklari kontseptsiyaga bo'ysundilar cheksiz kichik qattiq tanqid. Mishel Rol yangi hisob-kitoblar " ajoyib xatolar to'plami»; Volter bu hisob borligini isbotlab bo'lmaydigan narsalarni hisoblash va to'g'ri o'lchash san'ati ekanligini qattiq ta'kidladi. Hatto Gyuygens ham yuqori tartibli differentsiallarning ma'nosini tushunmaganligini tan oldi.
Parij Fanlar akademiyasida tahlilni asoslash masalalari bo'yicha tortishuvlar shu qadar shov-shuvga sabab bo'ldiki, bir vaqtlar Akademiya o'z a'zolariga bu mavzuda gapirishni taqiqlab qo'ydi (bu asosan Rol va Varignonga tegishli edi). 1706 yilda Rol o'z e'tirozlarini ochiqchasiga qaytarib oldi, ammo muhokamalar davom etdi.
1734 yilda mashhur ingliz faylasufi, episkop Jorj Berkli qisqartirilgan sarlavha ostida mashhur bo'lgan shov-shuvli risolani nashr etdi. Tahlilchi". Uning to'liq nomi: Zamonaviy tahlilning mavzusi, tamoyillari va xulosalari diniy marosimlar va e'tiqod qoidalariga qaraganda aniqroq idrok etilganmi yoki aniqroq chiqarilganmi yoki yo'qligini o'rganuvchi imonsiz matematikga qaratilgan tahlilchi yoki nutq.».
Tahlilchi cheksiz kichik hisobni aqlli va ko'p jihatdan adolatli tanqid qildi. Berkli tahlil usulini mantiqqa zid deb hisobladi va shunday deb yozgan edi: qanchalik foydali bo'lsa, u faqat taxminning bir turi sifatida qaralishi mumkin; epchillik, san'at, to'g'rirog'i, ayyorlik, lekin ilmiy isbotlash usuli sifatida emas". Berkli Nyutonning joriy miqdorlarning "tug'ilishi yoki yo'q bo'lishining boshida" ko'payishi haqidagi iborasini iqtibos qilib, kinoya bilan: " ular na chekli, na cheksiz kichik, na hatto hech narsa emas. Biz ularni o'lik kattalikdagi fantomlar deb atay olmadikmi?... Qanday qilib kattaligi bo'lmagan narsalar o'rtasidagi munosabat haqida gapirish mumkin?.. Ikkinchi yoki uchinchi oqimni [hosilani] hazm qila oladigan kishi, ikkinchi yoki uchinchisi. menga ilohiyotda biror narsadan ayb topayotgandek tuyuladi».
Bir lahzali tezlikni, ya’ni berilgan lahzadagi va berilgan nuqtadagi tezlikni tasavvur qilishning iloji yo‘q, deb yozadi Berkli, chunki harakat tushunchasi (cheklangan nolga teng bo‘lmagan) fazo va vaqt tushunchalarini o‘z ichiga oladi.
Qanday qilib tahlil to'g'ri natijalarga erishadi? Berkli bu o'zaro kompensatsiyaning analitik xulosalarida bir nechta xatolar mavjudligi bilan bog'liq degan xulosaga keldi va buni parabola misolida ko'rsatdi. Qizig'i shundaki, ba'zi yirik matematiklar (masalan, Lagrange) u bilan kelishgan.
Matematikadagi qat'iylik va unumdorlik bir-biriga xalaqit berganda paradoksal vaziyat yuzaga keldi. Noto'g'ri tushunchalar bilan noqonuniy harakatlardan foydalanishga qaramay, to'g'ridan-to'g'ri xatolar soni hayratlanarli darajada kam edi - sezgi yordam berdi. Va shunga qaramay, butun 18-asr davomida matematik tahlil tez rivojlandi va hech qanday asosga ega bo'lmadi. Uning samaradorligi hayratlanarli edi va o'zi uchun gapirdi, ammo differentsialning ma'nosi hali ham noaniq edi. Funktsiyaning cheksiz kichik o'sishi va uning chiziqli qismi ayniqsa tez-tez chalkashib ketgan.
18-asr davomida vaziyatni to'g'rilash uchun juda katta sa'y-harakatlar amalga oshirildi va ularda asrning eng yaxshi matematiklari qatnashdilar, ammo faqat Koshi 19-asrning boshlarida tahlil asoslarini ishonchli tarzda qura oldi. U asosiy tushunchalarni - chegara, yaqinlik, uzluksizlik, differensial va hokazolarni qat'iy belgilab berdi, shundan so'ng haqiqiy cheksiz kichiklar fandan yo'qoldi. Qolgan nozikliklarning ba'zilari keyinroq tushuntiriladi
2.4 teorema. Agar (x n ) va (y n ) ketma-ketliklari yaqinlashsa va x n ≤ y n, n > n 0 bo‘lsa, lim x n ≤ lim y n bo‘ladi.
lim xn = a bo‘lsin, |
limyn = b va a > b. Ta'rif bo'yicha 2.4 chegaralar |
||||||||||||||||||||
e = sonidagi ketma-ketliklar |
shunday N raqami mavjud |
||||||||||||||||||||
Shuning uchun n > max(n0 , N) yn< |
< xn , что противоречит |
||||||||||||||||||||
holat. |
|||||||||||||||||||||
Izoh. Agar (xn ), (yn ) ketma-ketliklar uchun yaqinlashsa |
|||||||||||||||||||||
hammasi n > n0 |
xn< yn , то можно утверждать лишь, что lim xn |
≤ limin. |
|||||||||||||||||||
Buni ko'rish uchun ketma-ketliklarni ko'rib chiqish kifoya
va yn = |
||||
Quyidagi natijalar to'g'ridan-to'g'ri 2.4 ta'rifidan kelib chiqadi.
2.5 teorema. Agar sonlar ketma-ketligi (x n ) yaqinlashsa va lim x n< b (b R), то N N: x n < b, n >N.
Natija. Agar ketma-ketlik (xn ) yaqinlashsa va lim xn 6= 0 bo'lsa, u holda
N N: sgn xn = sgn(lim xn ), n > N.
2.6 teorema. (x n ), (y n ), (z n ) ketma-ketliklar shartlarni qanoatlantirsin:
1) xn ≤ yn ≤ zn , n > n0 ,
2) ketma-ketliklar(x n ) va (z n ) yaqinlashadi va lim x n = lim z n = a.
Keyin ketma-ketlik (y n ) yaqinlashadi va lim y n = a.
2.1.3 Cheksiz kichik ketma-ketliklar
Ta'rif 2.7. Raqamli ketma-ketlik (x n ), agar u yaqinlashsa va lim x n = 0 bo'lsa, cheksiz kichik (qisqacha b.m) deyiladi.
Raqamlar ketma-ketligi chegarasining 2.4 taʼrifiga koʻra, 2.7 taʼrifi quyidagilarga ekvivalentdir:
Ta'rif 2.8. Sonli ketma-ketlik (x n ) cheksiz kichik deb ataladi, agar har qanday musbat e soni uchun N = N(e) son bo'lsa, shundayki, barcha n > N uchun bu ketma-ketlikning x n elementlari |x n | tengsizlikni qanoatlantirsa.< ε.
Shunday qilib, (xn) - b.m. e > 0 N = N(e) : n > N |xn |< ε.
2 va 3-misollardan va 1-izohdan 2.3 teoremaga kelib, biz shunday xulosaga kelamizki, keyin
izchillik ( |
q−n |
cheksizdir |
||||||||||||
Cheksiz kichik ketma-ketliklarning xossalari quyidagi teoremalar bilan tavsiflanadi.
2.7 teorema. Cheklangan sonli cheksiz kichik ketma-ketliklarning yig'indisi cheksiz kichik ketma-ketlikdir.
(xn ), (yn ) ketma-ketliklar cheksiz kichik bo'lsin. (xn + yn ) ham shunday bo'lishini ko'rsatamiz. Keling, e > 0 ni o'rnatamiz. Keyin raqam bor
N1 = N1 (e) shunday |
||||
|xn |< |
N > N1 , |
|||
va shunday N2 = N2 (e) soni mavjud |
||||
|yn|< |
N > N2 . |
|||
N = max(N1 , N2 ) bilan belgilang. n > N uchun (2.1) va (2.2) tengsizliklar amal qiladi. Shuning uchun n > N uchun
|xn + yn | ≤ |xn | + |yn |< 2 + 2 = ε.
Bu (xn +yn ) ketma-ketlikning cheksiz kichik ekanligini bildiradi. Cheklangan sonli cheksiz kichik ketma-ketliklarning yig'indisi haqidagi bayonot
qiymatlar induksiya bilan isbotlangan narsadan kelib chiqadi.
2.8 teorema. Cheksiz kichik ketma-ketlik va chegaralangan ketma-ketlikning mahsuloti cheksiz kichikdir.
(xn ) chegaralangan va (yn ) cheksiz kichik ketma-ketlik bo'lsin. Cheklangan ketma-ketlikning 2.6 ta'rifiga ko'ra M > 0 soni mavjud
|xn | ≤ M, nN. |
Biz ixtiyoriy e > 0 sonni tuzatamiz. (yn ) cheksiz kichik ketma-ketlik ekan, N = N(e) son mavjud
Shuning uchun, ketma-ketlik (xn yn ) cheksiz kichikdir.

Xulosa 1. Cheksiz kichik ketma-ketlik va yaqinlashuvchining ko'paytmasi cheksiz kichik ketma-ketlikdir.
Xulosa 2. Ikki cheksiz kichik ketma-ketlikning mahsuloti cheksiz kichik ketma-ketlikdir.
Cheksiz kichik ketma-ketliklardan foydalanib, konvergent ketma-ketlikning ta'rifini boshqacha ko'rish mumkin.
Lemma 2.1. A soni sonlar qatorining chegarasi (x n ) bo lishi uchun x n = a + a n , n N tasvirlanishi zarur va yetarli, unda (a n ) cheksiz kichik qatordir.
Zaruriyat. lim xn = a va R bo'lsin. Keyin
e > 0 N = N(e) N: n > N |xn − a|< ε.
Agar a = xn − a, n N qo‘ysak, u holda (an ) cheksiz kichik ketma-ketlik va xn = a + an , n N ekanligini olamiz.
Adekvatlik. Ketma-ketlik (xn ) shunday bo'lsinki, xn = a + a , n N va lim an = 0 bo'lgan a son mavjud bo'lsin. Ixtiyoriy musbat e sonni aniqlang. lim an = 0 bo'lgani uchun N = N(e) N son mavjud bo'lib, |an |< ε, n >N. Ya'ni, boshqa belgilarda n > N |xn − a|< ε. Это означает, что lim xn = a.
Keling, Lemma 2.1 ni bitta muhim misolga qo'llaymiz.
Lemma 2.2. lim n n = 1.
√ √
Hammasi uchun n > 1 n n > 1 bo‘lgani uchun n n = 1 + an , va a > 0 uchun
hammasi n > 1. Demak, n = (1 + a |
)n = 1 + na |
+an. |
|||||||||||||||
Barcha shartlar ijobiy bo'lgani uchun n |
|||||||||||||||||
e > 0 bo'lsin |
2/n< ε для всех n >2/e, keyin, sozlash |
||||||||||||||||
N = max(1, ), biz 0 ni olamiz< αn < ε, n >N. Shuning uchun,
ketma-ketlik (an ) cheksiz kichik va lemmaga ko'ra
2.1, lim n n = 1. √
Natija. Agar a > 1 bo'lsa, lim n a = 1.√ √
Tasdiqlash tengsizliklardan kelib chiqadi 1< n a ≤ n n , n >[a].
2.1.4 Ketma-ketlik arifmetikasi
Lemma 2.1 va cheksiz kichik ketma-ketliklarning xossalaridan foydalanib, konvergent ketma-ketliklardan arifmetik amallar yordamida olingan ketma-ketliklar chegaralari haqidagi teoremalarni olish oson.

|b| 3|b|
2 < |y n | < 2
2.9 teorema. (x n ) va (y n ) sonli ketma-ketliklar yaqinlashsin. Keyin bayonotlar amalga oshiriladi:
1) ketma-ketlik (x n ± y n) yaqinlashadi va
lim(xn ± yn ) = lim xn ± lim yn ;
2) ketma-ketlik (x n y n ) yaqinlashadi va
lim(xn yn ) = lim xn lim yn ;
3) agar lim y n 6= 0 bo'lsa, u holda x n /y n nisbati dan boshlab aniqlanadi.
ba'zi son, ketma-ketlik ( x n ) yaqinlashadi va
2.8-teorema va 1-sonli xulosaga ko‘ra (a bn ), (b an ), (an bn ) ketma-ketliklar cheksiz kichikdir. Teorema 2.7 bo'yicha ketma-ketlik (abn + ban + an bn ) cheksiz kichikdir. Lemma 2.1 orqali (2.5) vakillik 2-tasdiqni nazarda tutadi).
Keling, 3-bandga murojaat qilaylik). Faraz bo'yicha, lim yn = b 6= 0. 2.3-teorema asosida. ketma-ketlik (|yn |) yaqinlashadi va lim |yn | = |b| 6= 0. Demak, e = |b|/2 son berilgan bo‘lsa, N son borki, n > N bo‘ladi.
0 < | 2 b| = |b| −
Demak, yn =6 0 va 3|b|< y n < |b| , n >N.
Shunday qilib, xn /yn qismi barcha n > N uchun aniqlanadi va ketma-ketlik (1/yn ) chegaralanadi. Barcha n > N uchun farqni ko'rib chiqing
(anb − abn ). |
|||||||||||||||||||||
Keyingi ketma-ketlik |
anb |
aan |
cheksiz kichik, |
||||||||||||||||||
cheklangan. 2.8 teorema bo'yicha ketma-ketlik |
|||||||||||||||||||||
−b |
|||||||||||||||||||||
kichkina. Demak, Lemma 2.1 ga asosan 3) ta'kid isbotlangan. Xulosa 1. Agar ketma-ketlik (xn) yaqinlashsa, u holda har qanday uchun
xudoning c sonining ketma-ketligi (c · xn ) yaqinlashadi va lim(cxn ) = c · lim xn .
Cheksiz kichik funktsiyalar
%%f(x)%% funksiyasi chaqiriladi cheksiz kichik(b.m.) %%x \to a \in \overline(\mathbb(R))%% uchun, agar argument bunga intilganda funksiya chegarasi nolga teng bo'lsa.
b.m. haqida tushuncha. funktsiya o'z argumentidagi o'zgarish belgisi bilan uzviy bog'liqdir. Biz b.m haqida gapirishimiz mumkin. %%a \to a + 0%% va %%a \to a uchun - 0%% funktsiyalari. Odatda b.m. funksiyalar yunon alifbosining birinchi harflari bilan belgilanadi %%\alpha, \beta, \gamma, \ldots%%
Misollar
- %%f(x) = x%% funksiyasi b.m. %%x \to 0%% da, chunki uning %%a = 0%% da chegarasi nolga teng. Ikki tomonlama chegara bilan bir tomonlama chegara o'rtasidagi bog'liqlik teoremasiga ko'ra, bu funktsiya b.m. ham %%x \to +0%% va %%x \to -0%% bilan.
- Funktsiya %%f(x) = 1/(x^2)%% - b.m. %%x \to \infty%% (shuningdek, %%x \to +\infty%% va %%x \to -\infty%%) bilan.
Nolga teng bo'lmagan doimiy son, mutlaq qiymati qanchalik kichik bo'lmasin, b.m. funktsiyasi. Doimiy sonlar uchun yagona istisno nolga teng, chunki %%f(x) \equiv 0%% funksiyasi nol chegarasiga ega.
Teorema
%%f(x)%% funksiyasi kengaytirilgan son satrning %%a \in \overline(\mathbb(R))%% nuqtasida yakuniy chegaraga ega bo‘lsa, faqat %%b%% soniga teng. agar bu funktsiya ushbu sonning yig'indisiga teng bo'lsa %%b%% va b.m. %%\alpha(x)%% funksiyalari %%x \to a%% yoki $$ \exists~\lim\limits_(x \to a)(f(x)) = b \in \mathbb(R) bilan ) \Chapga o'q \left(f(x) = b + \alpha(x)\o'ng) \land \left(\lim\limits_(x \to a)(\alfa(x) = 0)\o'ng). $$
Cheksiz kichik funksiyalarning xossalari
Limitga o'tish qoidalariga ko'ra, %%c_k = 1~ \forall k = \overline(1, m), m \in \mathbb(N)%% uchun quyidagi gaplar bajariladi:
- Yakuniy sonning yig'indisi b.m. %%x \to a%% uchun funksiyalar f.m. %%x \to a%% bilan.
- B.m.ning istalgan sonining mahsuloti. %%x \to a%% uchun funksiyalar f.m. %%x \to a%% bilan.
b.m.ning mahsuloti. %%x \to a%% da funksiyalar va ba'zi bir teshilgan qo'shnilikda chegaralangan funksiya %%\stackrel(\circ)(\text(U))(a)%% a nuqtasi b.m. %%x \to a%% funktsiyasi bilan.
Ko'rinib turibdiki, doimiy funktsiyaning mahsuloti va b.m. %%x \to a%% da b.m. %%x \to a%% da funksiya.
Ekvivalent cheksiz kichik funksiyalar
Cheksiz kichik funksiyalar %%\alpha(x), \beta(x)%% uchun %%x \to a%% deyiladi. ekvivalent va %%\alpha(x) \sim \beta(x)%% agar yoziladi
$$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\limits_(x \to a)(\frac(\beta(x)) )(\alfa(x))) = 1. $$
b.m.ni almashtirish haqidagi teorema. funksiyalar ekvivalenti
%%\alfa(x), \alpha_1(x), \beta(x), \beta_1(x)%% b.m bo'lsin. funksiyalar %%x \to a%% va %%\alpha(x) \sim \alpha_1(x); \beta(x) \sim \beta_1(x)%%, keyin $$ \lim\limits_(x \to a)(\frac(\alpha(x))(\beta(x))) = \lim\ limits_(x \to a)(\frac(\alpha_1(x))(\beta_1(x))). $$
Ekvivalent b.m. funktsiyalari.
%%\alfa(x)%% b.m bo'lsin. %%x \to a%% da funksiyasi, keyin
- %%\sin(\alfa(x)) \sim \alfa(x)%%
- %%\displaystyle 1 - \cos(\alpha(x)) \sim \frac(\alpha^2(x))(2)%%
- %%\tan \alpha(x) \sim \alpha(x)%%
- %%\arcsin\alpha(x) \sim \alpha(x)%%
- %%\arctan\alpha(x) \sim \alpha(x)%%
- %%\ln(1 + \alfa(x)) \sim \alfa(x)%%
- %%\displaystyle\sqrt[n](1 + \alpha(x)) - 1 \sim \frac(\alpha(x))(n)%%
- %%\displaystyle a^(\alfa(x)) - 1 \sim \alfa(x) \ln(a)%%
Misol
$$ \begin(massiv)(ll) \lim\limits_(x \to 0)( \frac(\ln\cos x)(\sqrt(1 + x^2) - 1)) & = \lim\limits_ (x \to 0)(\frac(\ln(1 + (\cos x - 1))))(\frac(x^2)(4))) = \\ & = \lim\limits_(x \to) 0)(\frac(4(\cos x - 1))(x^2)) = \\ & = \lim\limits_(x \to 0)(-\frac(4 x^2)(2 x^ 2)) = -2 \end(massiv) $$
Cheksiz katta funksiyalar
%%f(x)%% funksiyasi chaqiriladi cheksiz katta(b.b.) %%x \to a \in \overline(\mathbb(R))%% uchun, agar funktsiya cheksiz chegaraga ega bo'lsa, chunki argument shunday qilishga intiladi.
b.m. b.b kontseptsiyasini bajaradi. funktsiya o'z argumentidagi o'zgarish belgisi bilan uzviy bog'liqdir. Biz b.b haqida gapirishimiz mumkin. funktsiyalari %%x \to a + 0%% va %%x \to a - 0%% gacha. "Cheksiz katta" atamasi funktsiyaning mutlaq qiymatini emas, balki uning ko'rib chiqilayotgan nuqta yaqinidagi o'zgarishi tabiatini anglatadi. Hech qanday doimiy son, mutlaq qiymatda qanchalik katta bo'lmasin, cheksiz katta emas.
Misollar
- Funktsiya %%f(x) = 1/x%% - b.b. %%x \to 0%% gacha.
- Funktsiya %%f(x) = x%% - b.b. %%x \to \infty%% da.
Ta'riflar shartlari $$ \begin(massiv)(l) \lim\limits_(x \to a)(f(x)) = +\infty, \\ \lim\limits_(x \to a)( f( x)) = -\infty, \end(massiv) $$
keyin ular haqida gapirishadi ijobiy yoki salbiy b.b. %%a%% funktsiyasida.
Misol
%%1/(x^2)%% funksiyasi musbat b.b. %%x \to 0%% gacha.
b.b. oʻrtasidagi bogʻliqlik. va b.m. funktsiyalari
%%f(x)%% bo'lsa b.b. %%x \to a%% funksiya bo'lsa, %%1/f(x)%% b.m.
%%x \to a%% bilan. %%\alfa(x)%% bo'lsa b.m. %%x \to a%% uchun %%a%% nuqtaning ba'zi teshilgan qo'shnisida nolga teng bo'lmagan funksiya, keyin %%1/\alfa(x)%% b.b. %%x \to a%% bilan.
Cheksiz katta funksiyalarning xossalari
Keling, b.b.ning bir qancha xususiyatlarini keltiramiz. funktsiyalari. Bu xususiyatlar to'g'ridan-to'g'ri b.b ta'rifidan kelib chiqadi. cheklangan chegaralarga ega boʻlgan funksiyalar va funksiyalarning xossalari, shuningdek, b.b. oʻrtasidagi bogʻlanish teoremasidan. va b.m. funktsiyalari.
- Cheklangan sonning hosilasi b.b. %%x \to a%% uchun funksiyalar b.b. %%x \to a%% da funksiyasi. Haqiqatan ham, agar %%f_k(x), k = \overline(1, n)%% b.b. %%x \to a%% da, so'ngra nuqtaning ba'zi teshilgan qo'shnilarida %%a%% %%f_k(x) \ne 0%% va bog‘lanish teoremasi bo‘yicha b.b. va b.m. funktsiyalari %%1/f_k(x)%% - b.m. %%x \to a%% da funksiyasi. Aniqlanishicha, %%\displaystyle\prod^(n)_(k = 1) 1/f_k(x)%% %%x \to a%% uchun b.m funksiyasi va %%\displaystyle\prod^( n )_(k = 1)f_k(x)%% — b.b. %%x \to a%% da funksiya.
- b.b.ning mahsuloti. %%x \to a%% da funksiyalar va %%a%% nuqtaning ba'zi teshilgan qo'shnilarida mutlaq qiymati musbat doimiydan katta bo'lgan funksiya a b.b. %%x \to a%% da funksiya. Xususan, b.b.ning mahsuloti. %%x \to a%% da funksiyalar va %%a%% nuqtada chekli nolga teng bo'lmagan chegaraga ega bo'lgan funksiya b.b bo'ladi. %%x \to a%% da funksiya.
Ikki b.b.ning yigʻindisi. %%x \to a%% da noaniqlik mavjud. Shartlar belgisiga qarab, bunday summaning o'zgarishi tabiati juda boshqacha bo'lishi mumkin.
Misol
%%f(x)= x, g(x) = 2x, h(x) = -x, v(x) = x + \sin x%% - b.b funktsiyalari bo'lsin. %%x \to \infty%% da ishlaydi. Keyin:
- %%f(x) + g(x) = 3x%% - b.b. %%x \to \infty%% da funksiya;
- %%f(x) + h(x) = 0%% - b.m. %%x \to \infty%% da funksiya;
- %%h(x) + v(x) = \sin x%%, %%x \to \infty%% gacha chegarasi yo'q.
%%a%% va b.b nuqtaning ba'zi bir teshilgan qo'shnisida chegaralangan funktsiya yig'indisi. %%x \to a%% da funksiyalar b.b. %%x \to a%% da funksiya.
Masalan, %%x - \sin x%% va %%x + \cos x%% funktsiyalari b.b. %%x \to \infty%% da.
